Question

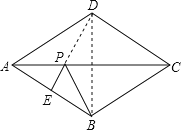
【题目】如图，菱形ABCD的周长为16，∠ADC=120，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是___________.

Answer 1

【答案】2

【解析】

连接BD，根据菱形的对角线平分一组对角可得∠BDA=∠ADC=60°，然后判断出△ABD是等边三角形，连接DE，根据轴对称确定最短路线问题，DE与AC的交点即为所求的点P，PE+PB的最小值=DE，然后根据等边三角形的性质求出DE即可得解．

解：如图，连接BD，

∵四边形ABCD是菱形，
∴∠BDA=∠ADC=×120°=60°，
∵AB=AD（菱形的邻边相等），
∴△ABD是等边三角形，
连接DE，∵B、D关于对角线AC对称，
∴DE与AC的交点即为所求的点P，PE+PB的最小值=DE，
∵E是AB的中点，
∴DE⊥AB，
∵菱形ABCD周长为16，
∴AD=16÷4=4，
∴DE=．
故答案为：2．