题目内容
【题目】如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点. 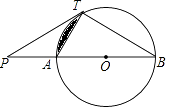
(1)求证:PT2=PAPB;
(2)若PT=TB= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】
(1)证明:连接OT.
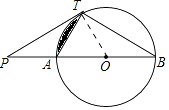
∵PT是⊙O的切线,
∴PT⊥OT,
∴∠PTO=90°,
∴∠PTA+∠OTA=90°,
∵AB是直径,
∴∠ATB=90°,
∴∠TAB+∠B=90°,
∵OT=OA,
∴∠OAT=∠OTA,
∴∠PTA=∠B,∵∠P=∠P,
∴△PTA∽△PBT,
∴ ![]() =
= ![]() ,
,
∴PT2=PAPB.
(2)∵TP=TB= ![]() ,
,
∴∠P=∠B=∠PTA,
∵∠TAB=∠P+∠PTA,
∴∠TAB=2∠B,
∵∠TAB+∠B=90°,
∴∠TAB=60°,∠B=30°,
∴tanB= ![]() =
= ![]() ,
,
∴AT=1,
∵OA=OT,∠TAO=60°,
∴△AOT是等边三角形,
∴S阴=S扇形OAT﹣S△AOT= ![]() ﹣
﹣ ![]() 12=
12= ![]() ﹣
﹣ ![]()
【解析】(1)连接OT,只要证明△PTA∽△PBT,可得 ![]() =
= ![]() ,由此即可解决问题;(2)首先证明△AOT是等边三角形,根据S阴=S扇形OAT﹣S△AOT计算即可;
,由此即可解决问题;(2)首先证明△AOT是等边三角形,根据S阴=S扇形OAT﹣S△AOT计算即可;
【考点精析】根据题目的已知条件,利用切线的性质定理和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

【题目】某中学九(2)班同学为了了解2019年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
月均用水量 | 频数 | 频率 |
| 6 | 0.12 |
| ________ | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | ________ |
| 2 | 0.04 |

请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)月均用水量的中位数落在第________小组;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?






