题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
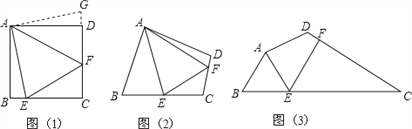
(1)如图1,若MP⊥CD,则∠BMP=___度;
(2)如图2,当P点在CD延长线上时,∠BMP=___(用α表示);
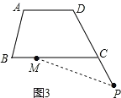
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

【答案】(1)150;(2)60°+α;(3)不成立.理由见解析.
【解析】
(1)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(2)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(3)根据两直线平行,同位角相等∠BCP,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解.
解:(1)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
∵MP⊥CD,
∴∠CMP=90°-∠C=90°-60°=30°,
∴∠BMP=180°-∠CMP=180°-30°=150°;
(2)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
在△CMP中,∠CMP=180°-∠C-∠MPD=180°-60°-α=120°-α,
∴∠BMP=180°-∠CMP=180°-(120°-α)=60°+α;
(3)不成立.
理由如下:∵AD∥BC,
∴∠BCP=∠ADC=120°,
在△CMP中,∠CMP=180°-∠BCP-∠MPD=180°-120°-α=60°-α,
∴∠BMP=180°-∠CMP=180°-(60°-α)=120°+α.

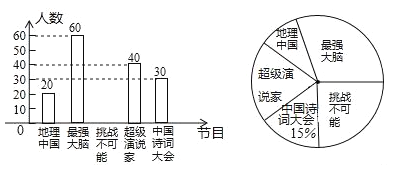
【题目】某班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班 50 名学生的处理方式进行统计,得出相关统计表和统计图.
组别 | A | B | C | D |
处理方式 | 迅速离开 | 马上救助 | 视情况而定 | 只看热闹 |
人数 | m | 30 | n | 5 |
请根据表图所提供的信息回答下列问题:
(1)统计表中的 m= ,n= ;
(2)补全频数分布直方图;
(3)若该校有 2000 名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?