题目内容
【题目】扑克牌游戏：小明背对小亮，让小亮按下列四个步骤操作：
第一步，分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌的张数相同；
第二步，从左边一堆拿出两张，放入中间一堆；
第三步，从右边一堆拿出一张，放入中间一堆；
第四步，左边一堆有几张牌，就从中间一堆拿出几张牌放入左边一堆.
这时，小明准确地说出了中间一堆牌现有的张数，聪明的你，你认为中间一堆牌的张数是多少？
【答案】5
【解析】
此题看似复杂，其实只是考查了整式的基本运算．把每堆牌的数量用相应的字母表示出来，列式表示变化情况即可找出最后答案．
解答：解：设第一步时候，每堆牌的数量都是x（x≥2）；
第二步时候：左边x-2，中间x+2，右边x；
第三步时候：左边x-2，中级x+3，右边x-1；
第四步开始时候，左边有（x-2）张牌，则从中间拿走（x-2）张，则中间所剩牌数为（x+3）-（x-2）=x+3-x+2=5．
所以中间一堆牌此时有5张牌．
【题型】填空题
【结束】
44
【题目】为什么总是1 089?
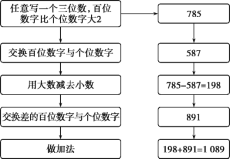
用不同的三位数再试几次,结果都是1 089吗?你能发现其中的原因吗?
【答案】结果都是1089,理由见解析
【解析】
设一个三位数为100a+10b+c,且a=c+2，可得原数为101c+10b+200，
交换百位数字与个位数字后的三位数为100c+10b+a，即为100c+10b+c+2=101c+10b+2，
所以大数减小数为198，可得交换前后的两个三位数，可得答案.
结果都是1 089.
原因:设一个三位数为100a+10b+c,且a=c+2,
所以100a+10b+c=100(c+2)+10b+c=101c+10b+200;
交换百位数字与个位数字后的三位数为100c+10b+a,即为100c+10b+c+2=101c+10b+2.
所以大数减小数为101c+10b+200-(101c+10b+2)=198.
所以将差的百位数字与个位数字交换后的三位数为891,198+891=1089.
阅读快车系列答案
