题目内容
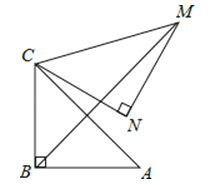
【题目】四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).若四边形OBCD是平行四边形时,那么∠OBA和∠ODA的数量关系是 . 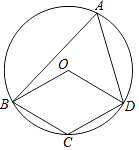
【答案】∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°
【解析】解: 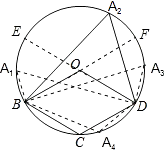
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°.
∵四边形OBCD是平行四边形,
∴∠C=∠BOD=2∠A,
∴∠A=60°,∠C=120°.
延长DO交⊙O于点E,延长BO交⊙O于点F.
①当点A1在 ![]() 上时,
上时,
∵∠CBA1+∠CDA1=180°,∠CBO+∠CDO=360°﹣120°﹣120°=120°,
∴∠CBO+∠OBA1+∠COD﹣∠ODA1=180°,
∴∠OBA1﹣∠ODA1=60°;
②当点A2在 ![]() 上时,
上时,
∵∠CBA2+∠CDA2=180°,∠CBO+∠CDO=360°﹣120°﹣120°=120°,
∴∠CBO+∠OBA2+∠COD+∠ODA2=180°,
∴∠OBA2+∠ODA2=60°;
③当点A3在 ![]() 上时,
上时,
∵∠CBA3+∠CDA3=180°,∠CBO+∠CDO=360°﹣120°﹣120°=120°,
∴∠CBO﹣∠OBA3+∠COD+∠ODA3=180°,
∴∠ODA3﹣∠OBA3=60°;
④当点A4在 ![]() 上时,
上时,
∠OBA4+∠ODA4=360°﹣120°﹣120°=120°.
综上所述,∠OBA和∠ODA的数量关系是:∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°.
所以答案是:∠OBA﹣∠ODA=60°或∠OBA+∠ODA=60°或∠ODA﹣∠OBA=60°或∠OBA+∠ODA=120°.
【考点精析】通过灵活运用平行四边形的性质和圆周角定理,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.

【题目】某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.下表是购买量x(千克)、付款金额y(元)部分对应的值,请你结合表格:
购买量x(千克) | 1.5 | 2 | 2.5 | 3 |
付款金额y(元) | 7.5 | 10 | 12 | b |
(1)写出a、b的值,a= b= ;
(2)求出当x>2时,y关于x的函数关系式;
(3)甲农户将18.8元钱全部用于购买该玉米种子,计算他的购买量.