Question

【题目】如图，在下列6×6的网格中，横、纵坐标均A（0，3），B（5，3）、C（1，5）都是格点在网格中仅用无刻度的直尺作图，保留作图痕迹．

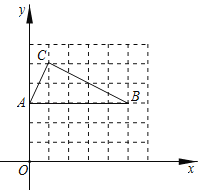
（1）画出以AB为斜边的等腰Rt△ABD（D在AB下方）；

（2）连接CD交AB于点E，则∠ACE的度数为　 　；

（3）在直线AB下方找一个格点F，连接CF，使∠ACF＝∠AEC，直接写出F点坐标　 　；

（4）由上述作图直接写出tan∠AEC的值　 　．

Answer 1

【答案】（1）见解析；（2）∠ACE＝45°；（3）（6，0）；（4）3

【解析】

（1）取格点M，N，连接AM，BN交于点D，点D即为所求．

（2）利用四点共圆的性质解决问题即可．

（3）取格点G，作直线CG可得点F．

（4）在Rt△ACF中，求出AF，AC即可解决问题．

（1）△ABD即为所求．

（2）∠ACE＝45°．

理由：∵∠ACB+∠ADB＝180°，

∴A，C，B，D四点共圆，

∵DA＝DB，

∴，

∴∠ACD＝∠BCD＝45°．

故答案为45°．

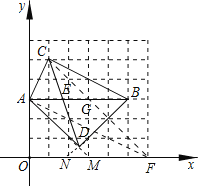
（3）点F即为所求．F（6，0）．

理由：△ACE，∠ACG中，

∵∠CAE＝∠CAG，∠ACE＝∠AGC＝45°，

∴∠AEC＝∠ACG，

即∠ACF＝∠AEC．

故答案为（6，0）．

（4）在Rt∠ACF中，tan∠ACF＝＝＝3，

∵∠ACF＝∠AEC，

∴tan∠AEC＝3．

故答案为3．