题目内容
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 的一个交点是
的一个交点是![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)设点![]() 是双曲线
是双曲线![]() 上一点,直线
上一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() .若
.若![]() ,结合图象,直接写出点
,结合图象,直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() .(2)满足条件的点
.(2)满足条件的点![]() 坐标为
坐标为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可解决问题.
(2)分两种情形①当点B在第四象限时,作AE⊥x轴于E,PF⊥x轴于F,由AE∥PF,得到![]() ,推出BF=1,②当点B在第一象限时,作AE⊥x轴于E,BF⊥x轴于F,由AE∥BF,得
,推出BF=1,②当点B在第一象限时,作AE⊥x轴于E,BF⊥x轴于F,由AE∥BF,得![]() ,推出BF=1,由此即可解决问题.
,推出BF=1,由此即可解决问题.
解:(1)把点![]() 的再把代入
的再把代入![]() 得到
得到![]() ,
,
再把![]() 的再把代入
的再把代入![]() ,
,![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() .
.
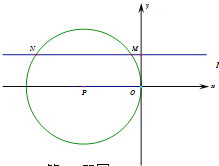
(2)①当点![]() 在第三象限时,如图1,作
在第三象限时,如图1,作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②当点![]() 在第一象限时,如图2,作
在第一象限时,如图2,作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
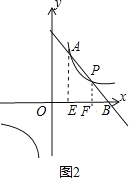
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,满足条件的点![]() 坐标为
坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目