题目内容
【题目】已知：四边形 ABCD 内接于⊙O，连接 AC、BD，∠BAD+2∠ACB=180°．
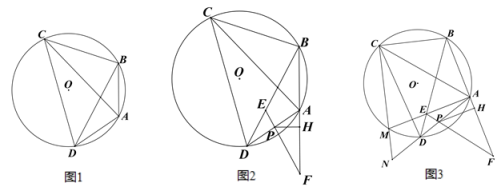
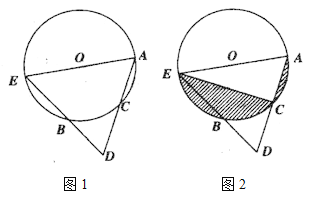
（1）如图 1，求证：点 A 为弧 BD 的中点；
（2）如图 2，点 E 为弦 BD 上一点，延长 BA 至点 F，使得 AF=AB，连接 FE 交 AD 于点 P，过点 P 作 PH⊥AF 于点 H，AF=2AH+AP，求证：AH:AB=PE:BE；
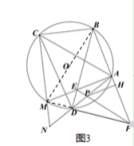
（3）在（2）的条件下，如图 3，连接 AE，并延长 AE 交⊙O 于点 M，连接 CM，并延长 CM 交 AD 的延长线于点 N，连接 FD，∠MND=∠MED，DF=12﹒sin∠ACB，MN=
，求 AH 的长．
【答案】（1）见解析；（2）见解析；（3）
．
【解析】
（1）根据圆的内接四边形的性质可得∠BAD+∠BCD=180°，然后结合已知条件即可证出∠ACB=∠ACD，从而证出结论；
（2）在HF上取点G，使HG=HA，连接PG、AE，根据垂直平分线的性质可得AP=GP，结合已知条件可得，GP=GF，结合三线合一证出EA⊥BF，再证出EA∥PH，根据平行线分线段成比例定理和等量代换即可得出结论；
（3）连接MB和MD，先利用等角对等边证出MN=MD=
，然后证出△BDF为直角三角形，∠BDF=90°，即可得出BF=12，然后证出△AFM∽△DFB，列出比例式即可求出DF，再根据勾股定理即可求出BD、BM，设AH=x，再利用相似三角形的判定及性质列出比例式即可求出结论．
解：（1）∵四边形 ABCD 内接于⊙O，
∴∠BAD+∠BCD=180°
∵∠BAD+2∠ACB=180°
∴∠BCD=2∠ACB
∴∠ACB=∠ACD
∴
即点 A 为弧 BD 的中点；
（2）在HF上取点G，使HG=HA，连接PG、AE
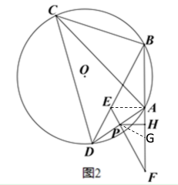
∵PH⊥AF
∴PH垂直平分AG
∴AP=GP
∴∠PAG=∠PGA
∵
∴∠ADB=∠ABD
∴∠PAG=∠ADB＋∠ABD=2∠ABD
∵AF=2AH+AP，AF=AH＋HG＋GF=2AH＋GF
∴AP=GF
∴GP=GF
∴∠GPF=∠F
∴∠PGA=∠GPF＋∠F=2∠F
∴∠ABD=∠F
∴EB=EF
∵AF=AB，
∴EA⊥BF
∴EA∥PH
∴AH：AF = PE：EF
∴AH:AB=PE:BE；
（3）连接MB和MD
∵
∴
∵
∴
∴
∴MN=MD=
∵，AB=AF
∴AB=AD=AF
∴∠ABD=∠ADB，∠ADF=∠AFD
∴∠ABD＋∠AFD=∠ADB＋∠ADF=∠BDF
∴△BDF为直角三角形，∠BDF=90°
∵
∴BF=12
∴AB=AD=AF=6
由（2）知：∠EAB=90°
∴∠MDB=90°
∴∠MDB＋∠BDF=180°
∴M、D、F三点共线
∵∠AFM=∠DFB，∠FAM=∠FDB=90°
∴△AFM∽△DFB
∴
即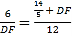
解得：DF=
或-10（不符合实际，舍去）
根据勾股定理可得BD=
BM=
设AH=x，由（2）知：AP=AF－2AH=6－2x
由圆的内角四边形的性质可得：∠PAH=∠BMD
∵∠AHP=∠MDB=90°
∴△AHP∽△MDB
∴
即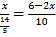
解得：x=
即
