��Ŀ����
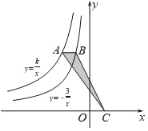
����Ŀ����֪������x�Ķ��κ���y��ax2��2ax��a��0���Ķ���ΪC����x�ύ�ڵ�O��A������x��һ�κ���y����ax��a��0����
��1����˵����C��һ�κ�����ͼ���ϣ�
��2���������㣨k��y1������k+2��y2����k��0����2�����ڶ��κ�����ͼ���ϣ��Ƿ��������k������![]() ��������ڣ������k��ֵ����������ڣ���˵�����ɣ�
��������ڣ������k��ֵ����������ڣ���˵�����ɣ�
��3������E�Ƕ��κ���ͼ����һ���㣬E��ĺ�������n���ҩ�1��n��1������E��y���ƽ���ߣ���һ�κ���ͼ���ڵ�F����0��a��2ʱ�����߶�EF�����ֵ��
���𰸡�(1)����������2�����ڣ�����k��ֵΪ��4����3��EF�����ֵ��4��
��������
��1����������κ���y��ax2��2ax��a��x��1��2��a����C��1����a������x��1ʱ��һ�κ���ֵy����a���Ե�C��һ�κ���y����ax��ͼ���ϣ�
��2�����ڣ����㣨k��y1������k+2��y2����k��0����2��������κ�������ʽ����a��k��ʾ��y1��y2����Ϊ����![]() ,��y1��y2���������ɵù���k�ķ��̣��ⷽ�̼��鼴�����k��ֵ.
,��y1��y2���������ɵù���k�ķ��̣��ⷽ�̼��鼴�����k��ֵ.
��3��������������ۣ��ٵ���1��n��0ʱ��EF��yE��yF��an2��2an������an����![]() �ڵ�0��n��1ʱ��EF��yF��yE����an����an2��2an����
�ڵ�0��n��1ʱ��EF��yF��yE����an����an2��2an����![]()
��1���߶��κ���y��ax2��2ax��a��x��1��2��a��
�ඥ��C��1����a����
�ߵ�x��1ʱ��һ�κ���ֵy����a
���C��һ�κ���y����ax��ͼ���ϣ�
��2�����ڣ�
�ߵ㣨k��y1������k+2��y2����k��0����2�����ڶ��κ�����ͼ���ϣ�
��y1��ak2��2ak��y2��a��k+2��2��2a��k+2����
������![]()
��![]() ��
��
�������� ![]() ��
��
��![]()
��![]() ��
��
���k����4��
�����飺k����4��ԭ���̵ĸ���
������k��ֵΪ��4��
��3���ߵ�E�Ƕ��κ���ͼ����һ���㣬
��E��n��an2��2an����
��EF��y�ᣬF��һ�κ���ͼ���ϣ���F��n����an����
�ٵ���1��n��0ʱ��EF��yE��yF��an2��2an������an����![]()
��a��0��
�൱n����1ʱ��EF�����ֵ�������ֵ��2a��
�֡�0��a��2��
��0��2a��4����EF�����ֵ��4��
�ڵ�0��n��1ʱ��EF��yF��yE����an����an2��2an����![]() ��ʱEF�����ֵ��
��ʱEF�����ֵ��![]() ��
��
�֡�0��a��2��
��0��![]() ��
��![]() ����EF�����ֵ��
����EF�����ֵ��![]() ��
��
����������EF�����ֵ��4��