题目内容
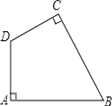
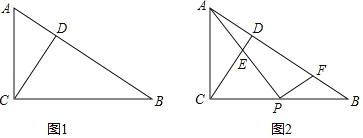
【题目】在△ABC中，∠ACB＝90°，CD为高，BC＝nAC
（1）如图1，当n＝
时，则
的值为 ；（直接写出结果）
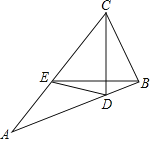
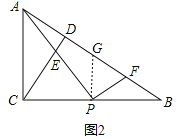
（2）如图2，点P是BC的中点，过点P作PF⊥AP交AB于F，求
的值；（用含n的代数式表示）
（3）在（2）的条件下，若PF＝BF，则n＝ ．（直接写出结果）
【答案】（1）
；（2）
；（3）
【解析】
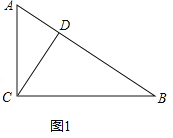
（1）设AC＝2k，BC＝3k，求出AD，BD即可解决问题．
（2）过点P作PG∥AC交AB于点G．证明△PCE∽△PGF，即可解决问题．
（3）设PF＝x，AP＝2nx，利用勾股定理构建方程求出n即可．
解：（1）如图1中，
，
可以假设
，
，
，
，
，
，
，
，
，
故答案为；
（2）过点
作
交
于点
．
，
，
，
，
，
，
，
，
又
，
，
，
，
，
又点是
的中点，
，
；
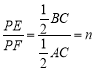（3）由（2）可知
，则可以假设
，
，
，
，则
，则
，
，
，则
，
又
，则
，
在Rt△APF中，
，
则
，
，
故答案为．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
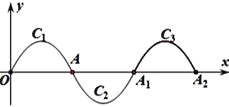
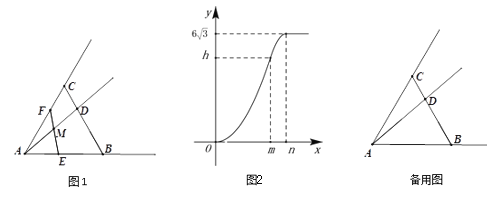
【题目】请你用学习“一次函数”时积累的经验和方法研究函数
的图象和性质，并解决问题．
完成下列步骤，画出函数的图象；
列表、填空；
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
描点：
连线
观察图象，当x______时，y随x的增大而增大；
结合图象，不等式
的解集为______．
