题目内容
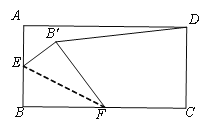
【题目】如图，矩形ABCD中，AD＝4，AB＝2．点E是AB的中点，点F是BC边上的任意一点（不与B、C重合），△EBF沿EF翻折，点B落在B'处，当DB'的长度最小时，BF的长度为________．
【答案】
【解析】
根据题意可知当FB'⊥DE时，DB'的长度最小，则根据勾股定理求出DE=
，设BF=x，根据折叠的性质可得B’E=1, B’F=x,则DB'=-1，FC=4-x,再根据DF是两个直角三角形的斜边，可根据勾股定理列出方程即可求解.
如图，当FB'⊥DE时，DB'的长度最小，
∵点E是AB的中点，
∴AE=BE=
=1
∴DE=
设BF=x，
∵折叠，∴B’E=1, B’F=x,
故DB'=-1，FC=4-x,
在Rt△DCF和Rt△B’DF中，
DF2=
即
解得x=
即BF=
故填：.
练习册系列答案
相关题目
