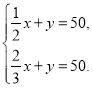Question

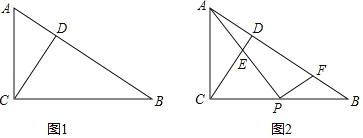
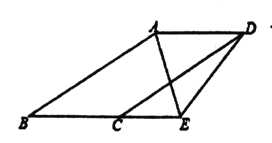
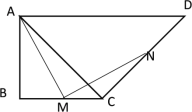
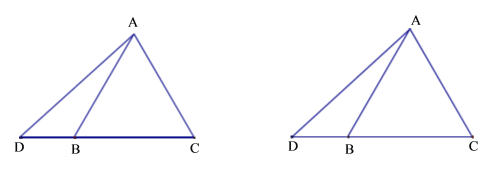
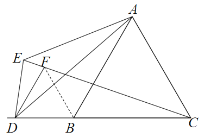
【题目】如图，在等边△ABC中，点D 是边CB延长线上一动点(BD<BC)，连接AD，点B 关于直线AD的对称点为E，过D 作DF//AB交CE于点F．

（1）依题意补全图形；

（2）求证：AD=CF；

（3）当∠DCE=15°时，直接写出线段AD，EF，BC之间的数量关系．

Answer 1

【答案】（1）见详解；（2）见详解；（3）EF+AD=BC，理由见详解

【解析】

（1）依据题意画出相应图形即可；

（2）连接FB，先DE＝DF，再证等边三角形DFB，最后通过证△DBA≌△FBC即可得证；

（3）先证△AEC为等腰直角三角形，再利用勾股定理即可得到AD，EF，BC之间的数量关系．

（1）解：如图即为所求，

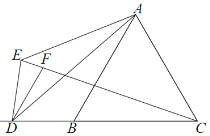
（2）证明：如图，连接FB，

∵点E、点B关于AD对称，

∴△ADE≌△ADB，

∴∠AED＝∠ABD，AE＝AB，

∵△ABC为等边三角形，

∴AB＝AC＝BC，∠ABC＝∠ACB＝∠BAC＝60°，

∴AE＝AC，

∴∠AEC＝∠ACE，

∵∠AED＝∠ABD，

∴∠AEC＋∠DEF＝∠BAC＋∠ACE＋∠DCF，

∴∠DEF＝∠BAC＋∠DCF＝60°＋∠DCF，

∵DF∥AB，

∴∠FDB＝∠ABC＝60°，

∴∠DFE＝∠FDB＋∠DCF＝60°＋∠DCF，

∴∠DFE＝∠DEF，

∴DE＝DF，

∴DB＝DF，

又∵∠FDB＝60°，

∴△BDF为等边三角形，

∴∠DBF＝∠ABC＝60°，DB＝FB，

∴∠DBA＝∠FBC＝120°，

在△DBA与△FBC中，

∴△DBA≌△FBC（SAS）

∴AD＝CF．

（3）解：∠ACB＝60°，∠DCE＝15°，

∴∠AEC＝∠ACE＝45°

∴∠EAC＝90°，

在Rt△ACE中，AE2＋AC2＝EC2，

∴EC2＝2AC2，

∴EC＝AC，

即EF＋FC＝AC，

又∵FC＝AD，AC＝BC，

∴EF＋AD＝BC．