题目内容
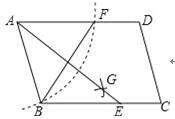
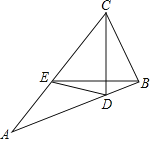
【题目】如图,在△ABC中,点D,E分别为AB,AC边上一点,且BE=CD,CD⊥BE.若∠A=30°,BD=1,CE=2![]() ,则四边形CEDB的面积为_____.
,则四边形CEDB的面积为_____.
【答案】![]()
【解析】
作辅助线![]() ,
,![]() ,由两直线垂直得
,由两直线垂直得![]() ,角角边证明△CKD≌△BHE,其性质得
,角角边证明△CKD≌△BHE,其性质得![]() ;设
;设![]() ,根据直角三角的性质,线段的和差得
,根据直角三角的性质,线段的和差得![]() ,
,![]() ,
,![]() ;建立等量关系
;建立等量关系![]() ,求得
,求得![]() ,
,![]() ,最后由勾股定理,面积公式求得四边形
,最后由勾股定理,面积公式求得四边形![]() 的面积为
的面积为![]() .
.
解:分别过点C、E两点作CK⊥AB,EH⊥AB
交AB于点K和点H,设CK=x,如图所示:

∵CD⊥BE,
∴∠BMD=90°,
∴∠EBH+∠CDB=90°,
同理可得:∠EBH+∠BEH=90°,
∴∠CDB=∠BEH,
又∵CK⊥AB,EH⊥AB,
∴∠CKD=∠BHE=90°,
在△CKD和△BHE中,
 ,
,
∴△CKD≌△BHE(AAS),
∴DK=EH,
又∵Rt△AKC中,∠A=30°,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]() ,
,
![]()
![]()
![]()
![]()
![]() .
.
故答案为![]() .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目