题目内容
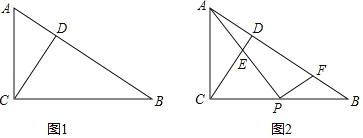
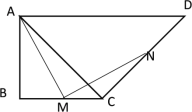
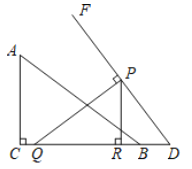
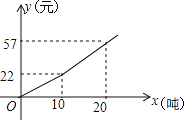
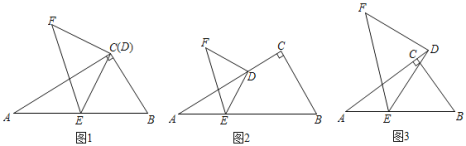
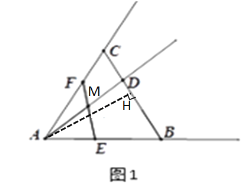
【题目】如图1,△ABC是等边三角形,点D在BC上,BD=2CD,点F是射线AC上的动点,点M是射线AD上的动点,∠AFM=∠DAB,FM的延长线与射线AB交于点E,设AM=x,△AME与△ABD重叠部分的面积为y,y与x的函数图象如图2所示(其中0<x≤m,m<x<n,x≥n时,函数的解析式不同).
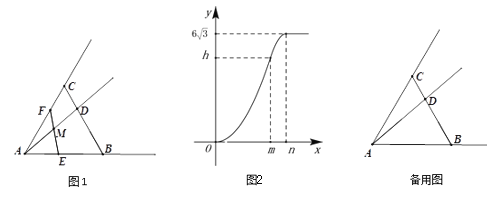
(1)填空:AB=_______;
(2)求出y与x的函数关系式,并求出x的取值范围.
【答案】(1)6;(2)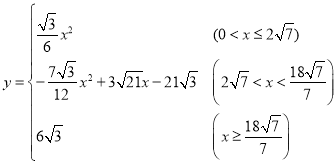
【解析】
(1)作高![]() ,由图象得出△ABD的面积,再由BD=2CD,得出△ABC的面积,利用三角形的面积公式求解即可;
,由图象得出△ABD的面积,再由BD=2CD,得出△ABC的面积,利用三角形的面积公式求解即可;
(2)先求出![]() ,
,![]() ,
,![]() ,
,![]() 的值,再利用勾股定理可得AD的值,再利用三角形相似,分类讨论,求解即可.
的值,再利用勾股定理可得AD的值,再利用三角形相似,分类讨论,求解即可.
(1)解:如图1,过点A作AH⊥BC,垂足为H,则![]() ,
,![]() ,由图象可知
,由图象可知![]() .
.
由![]() ,可知
,可知![]() ,
,![]() .
.
![]() 是等边三角形,可知
是等边三角形,可知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
得![]() .
.
(2)解:如图2,作高![]() ,则
,则![]() ,
,![]() ,由图象可知
,由图象可知![]() .
.

由![]() ,可知
,可知![]() ,
,![]() .
.
![]() 是等边三角形,可知
是等边三角形,可知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
得![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
由勾股定理可得,![]() .
.
由![]() ,可得
,可得![]() ,
,![]() ,
,![]() ,
,![]() .
.
当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() .
.
当![]() 时,如图1,
时,如图1,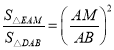 ,
,![]() ,
,![]() .
.
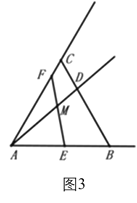
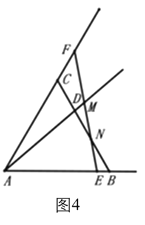
当![]() 时,如图4,
时,如图4,![]() ,
,![]() ,
,![]() .
.
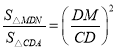 ,
,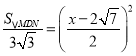 ,
,![]() .
.

![]() .
.
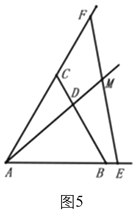
当![]() 时,如图5,
时,如图5,![]() .
.
综上,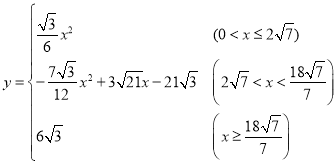 .
.

练习册系列答案
相关题目