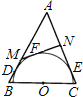题目内容
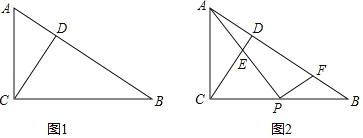
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() ,连接
,连接![]() .
.

(1)求证:![]() .
.
(2)填空:
①已知![]() ,当
,当![]() _________时,
_________时,![]() .
.
②连接![]() 、
、![]() 、
、![]() .当
.当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 是菱形.
是菱形.
【答案】(1)见解析
(2)①8;②30°
【解析】
(1)连接OD,因EF是圆的切线,则OD⊥EF.再通过内错角相等,证AF∥OD即可;
(2)①利用点C是AF的中点,证CB是AEF的中位线,从而求得BE的长;
(2)②利用菱形的性质,证ODB是正三角形,进而推导出∠E的大小.
(1)如下图,链接OD
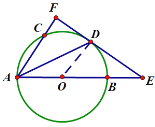
∵EF是O的切线
∴OD⊥EF
∵点D是![]() 的中点
的中点
∴∠CAD=∠DAB
∵OA=OD=r
∴∠DAB=∠ADO
∴∠CAD=∠ADO
∴AF∥OD
∴AF⊥EF
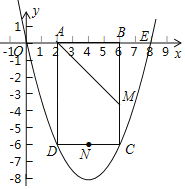
(2)①如下图,连接CB
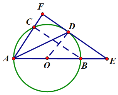
∵AB是O的直径,∴∠ACB=90°
∵AF⊥EF,∴EF∥CB
∵点C是AF的中点,∴CB是△AFE的中位线
∴BE=AB=8
(2)②如下图,连接CO、CD
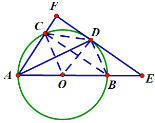
∵四边形OCDB是菱形,∴OB=DB
∵OD=OB,∴OD=OB=DB,∴△ODB是等边三角形
∴∠DOB=60°
∵AF∥OD,∴∠FAE=60°
∴∠E=30°

练习册系列答案
相关题目