题目内容
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
A.2sB.4sC.2s或4sD.2s或4.5s
【答案】D
【解析】
先根据时间和速度确定两动点P和Q的路程:AP=BQ=t,根据直角三角形30度的性质得AB的长,分两种情况:当∠APQ=90°和∠AQP=90°,根据AQ=2AP和AP=2AQ列方程可得结论.
解:由题意得:AP=BQ=t,
Rt△ABC中,∠C=90°,∠B=30°,
∴∠A=60°,
∴AC=3,
∴AB=2AC=6,
∴当△APQ是直角三角形时,有两种情况:
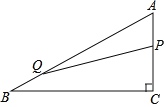
①当∠APQ=90°时,如图1,∠AQP=30°,
∴AQ=2AP,
∴6﹣t=2t,
t=2;
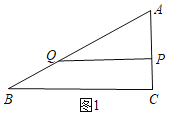
②当∠AQP=90°时,如图2,
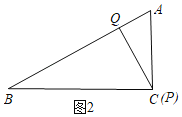
当0<t≤3时,AP=2AQ,即t=2(6﹣t),
t=4(不符合题意),
当t>3时,P与C重合,则AQ=![]() =6﹣t,
=6﹣t,
t=4.5,
综上,t的值为2s或4.5s;
故选:D.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目