题目内容
【题目】图![]() 是一个长为
是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线剪开分成四块小长方形,然后按图
的长方形,沿图中虚线剪开分成四块小长方形,然后按图![]() 的形状拼成一个正方形.(
的形状拼成一个正方形.(![]() )
)
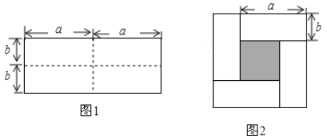
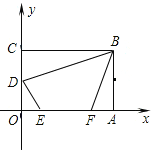
(1)图2的阴影部分的正方形的边长是____.
(2)用两种不同的方法求图中阴影部分的面积.
(方法![]() )
)![]() 阴影=____________________;
阴影=____________________;
(方法![]() )
)![]() 阴影=____________________;
阴影=____________________;
(3)利用(方法![]() )(方法
)(方法![]() )中两个代数式之间存在的等量关系,解决问题:若
)中两个代数式之间存在的等量关系,解决问题:若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;
;![]() (3)
(3)![]()
【解析】
(1)观察图2可知:阴影部分的正方形的边长是(a-b);
(2)【方法![]() 】图2中阴影部分为边长为(a-b)的正方形,利用正方形的面积公式可得出S阴影=(a-b)2;【方法
】图2中阴影部分为边长为(a-b)的正方形,利用正方形的面积公式可得出S阴影=(a-b)2;【方法![]() 】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,利用正方形及长方形的面积公式可得出S阴影=(a+b)2-4ab;
】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,利用正方形及长方形的面积公式可得出S阴影=(a+b)2-4ab;
(3)由阴影部分的面积相等可得出:(a+b)2-4ab=(a-b)2;据此可得出(x-y)2=(x+y)2-4xy,代入![]() 即可得出结论.
即可得出结论.
解:(1)根据题意得:图2的阴影部分的正方形的边长是(a-b).
故答案为:a-b;
(2)【方法![]() 】图2中阴影部分为边长为(a-b)的正方形,
】图2中阴影部分为边长为(a-b)的正方形,
∴S阴影=(a-b)2;
【方法![]() 】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,
】图2中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,
∴S阴影=(a+b)2-4ab.
故答案为:(a-b)2;(a+b)2-4ab.
(3)由(2)可知:(a+b)2-4ab=(a-b)2.
∴(x-y)2=(x+y)2-4xy
=102-4×16,
=36,
∴x-y =![]() ,
,

【题目】小张上星期六买进某公司的股票2000股,每股30元,下表是本周内每日该股票的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 |
|
|
|
|
|
|
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?
(3)请用拆线统计图表示该股票这六天的涨跌情况.(请在已设计好的坐标纸里画图)
(4)已知小张买过股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如小张在星期六收盘时将股票全部卖出,它的收益情况如何?