题目内容
【题目】如图，在平面直角坐标系中，一次函数y=kx+ b的图象分别与x轴和y轴交于点A、B(0，-2)，与正比例函数y=x的图象交于点C(m，2)．
(1)求m的值和一次函数的解析式；
(2)求△AOC的面积；
(3)直接写出使函数y =kx +b的值大于函数y=x的值的自变量x的取值范围．
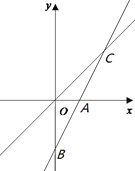
【答案】(1)m=2；y =2x﹣2；(2)S△AOC=1；(3)x＞2.
【解析】
(1)把C(m，2)代入y=x得m=2，可得C的坐标，且已知B点的坐标，即可求得一次函数解析式为y = 2x﹣2.
(2) 把y=0代入y=2x﹣2得x=1，则可得A点坐标，即可求得△AOC的面积.
(3) 根据一次函数图形，可知y =kx +b的值大于函数y=x的值，即为自变量x的取值范围是x＞2．
解：(1)把C(m，2)代入y=x得m=2，
则点C的坐标为(2，2)，
把C(2，2)，B(0, -2)代入y = kx + b得
解得
所以一次函数解析式为y = 2x﹣2；
(2)把y=0代入y=2x﹣2得x=1，则A点坐标为(1，0)，
所以S△AOC=
×2×1=1；
(3)根据一次函数图形，可知y =kx +b的值大于函数y=x的值，即为自变量x的取值范围是x＞2．
【题目】股民李明上星期六买进春兰公司股票1000股，每股27元.下表为本周内每日该股票的涨跌情况（单位：元）（注：本周一股票涨跌是在上周六的基础上，用正数记股价比前一日上升数，用负数记股价比前一日下降数）
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 | +2 |
（1）星期三收盘时，每股是多少元？
（2）本周内最高价是每股多少元？最低价每股多少元？
（3）己知李明买进股票时付了0.15%的手续费，卖出时需付成交额0.15%的手续费和0.1%的交易税，如果李明在星期六收盘前将全部股票卖出，他的收益情况如何？
