��Ŀ����
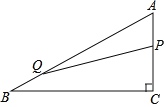
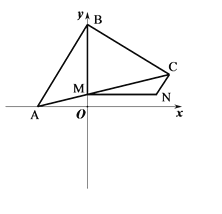
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�A��x�Ḻ������һ���㣬һ����B��ԭ���������y���������˶�����BΪֱ�Ƕ��㣬������ֱ����������ABC��
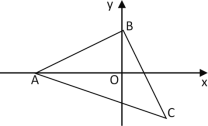
��1�� ��B�� �˶�2���ӣ�C������Ϊ��2��-2������A������ꣻ
��2�� ��ͼ��B��ӣ�1���е�λ�ó��������˶��ٶȲ��䣬���˶�2���ӣ�E��ԭB���ϣ���AE��OD��AE����x���ƽ����DB��D�㣬��D������
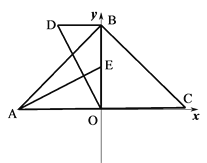
��3�� ��B�ӣ�2����λ�ó��������˶�����ͼAC��y����M��MN��y�ᣬ��BM=MN����CN�����ʣ�AB��CN�Ƿ���ij��ȷ����λ�ù�ϵ����֤����
���𰸡���1��A����4��0������2��D����2��4������3��AB��NC��
��������
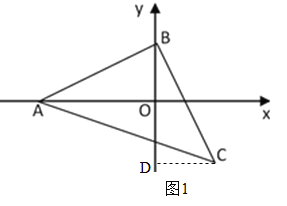
��1����C��CD��y����D��ͨ��֤����AOB�ա�BDC���õ�OB=CD��AO=BD����C�����꣬�õ�CD=2��OD=2�����ɵó����ۣ�
��2���ɣ�1���õ�OA��OE�ij��������õ�OA=BO��ͨ��֤����AOE��OBD���õ�OE=BD=2�����ɵó����ۣ�
��3����B��BH��AC��H����N��NG��AC��G����֤����BHM�ա�MGN���õ�BH=MG��MH=NG����֤��MH=GC�����������õ�GN=GC�����CGN�ǵ���ֱ�������Σ����С�NCG=��BAC�����ɵó����ۣ�
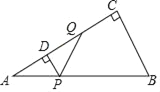
��1����ͼ1����C��CD��y����D�����DBC+��BCD=90�㣮
�ߵ���ֱ����������ABC����AB=CB����ABC=90�㣬���ABD+��CBD=90�㣬���ABD=��BCD��
�ߡ�AOB=��BDC=90�㣬���AOB�ա�BDC����OB=CD��AO=BD��
��C��������2��-2������CD=2��OD=2����AO=BD=BO+OD=CD+OD=2+2=4����A����4��0����
��2���ɣ�1����֪��OA=4��OE=BE=2����OB=4����OA=BO��
��OD��AE�����EAO+��AOD=90�㣮
�ߡ�AOD+��DOB=90�㣬���EAO=��DOB��
��DB��x�ᣬ���DBO=��EOA=90�㣮
�ڡ�AOE�͡�OBD�У��ߡ�EAO=��DOB��OA=BO����AOE=��OBD=90�㣬���AOE��OBD����OE=BD=2����D����2��4����
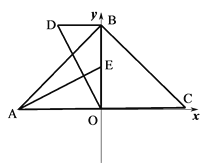
��3�� AB��NC���������£�
��B��BH��AC��H����N��NG��AC��G�����BHM=��MGN=90�㣬��HBM+��BMH=90�㣮
��MN��y�ᣬ���BMH+��NMG=90�㣬���HBM=��GMN��
�ڡ�BHM�͡�MGN�У��ߡ�HBM=��GMN����BHM=��MGN��BM=MN�����BHM�ա�MGN����BH=MG��MH=NG��
�ߡ�ABC�ǵ���ֱ�������Σ�BH��AC�����BAC=45�㣬BH=HC����MG=HC����MH+HG=HG+GC����MH=GC����GN=GC�����CGN�ǵ���ֱ�������Σ����NCG=45�㣬���NCG=��BAC����AB��NC��


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�����Ŀ��������������ˮƽ����ߣ����ýγ�Խ��Խ��ؽ����ͥ��С����������һ��С�γ�����������¼��7����ÿ����ʻ��·�̣����������50kmΪ��������50km�ļ�Ϊ��+��������50km�ļ�Ϊ���������պ�50km�ļ�Ϊ��0����
��һ�� | �ڶ��� | ������ | ������ | ������ | ������ | ������ | |
·�̣�km�� | ��8 | ��11 | ��14 | 0 | ��16 | +41 | +8 |
��1�������������ƽ��ÿ����ʻ����ǧ�ף�
��2����ÿ��ʻ100km��������6�������ͼ�6.2Ԫ/���������С����һ���£���30��ƣ������ͷ����Ƕ���Ԫ��
����Ŀ���������������������������˾��Ʊ1000�ɣ�ÿ��27Ԫ.�±�Ϊ������ÿ�ոù�Ʊ���ǵ��������λ��Ԫ����ע������һ��Ʊ�ǵ������������Ļ����ϣ��������ǹɼ۱�ǰһ�����������ø����ǹɼ۱�ǰһ���½�����
���� | һ | �� | �� | �� | �� | �� |
ÿ���ǵ� | +4 | +4.5 | -1 | -2.5 | -6 | +2 |
��1������������ʱ��ÿ���Ƕ���Ԫ��
��2�������������ÿ�ɶ���Ԫ����ͼ�ÿ�ɶ���Ԫ��
��3����֪���������Ʊʱ����0.15%�������ѣ�����ʱ�踶�ɽ���0.15%�������Ѻ�0.1%�Ľ���˰���������������������ǰ��ȫ����Ʊ�������������������Σ�