Question

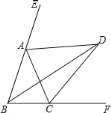
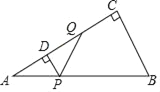
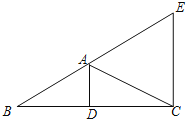
【题目】如图，在△ABC中，AD是边BC上的中线，∠BAD=∠CAD，CE∥AD，CE交BA的延长线于点E，BC=8，AD=3．

（1）求CE的长；

（2）求证：△ABC为等腰三角形．

（3）求△ABC的外接圆圆心P与内切圆圆心Q之间的距离．

Answer 1

【答案】（1）CE=6；（2）证明见解析；（3）△ABC的外接圆圆心P与内切圆圆心Q之间的距离为．

【解析】（1）证明AD为△BCE的中位线得到CE=2AD=6；

（2）通过证明△ABD≌△CAD得到AB=AC；

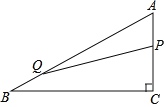
（3）如图，连接BP、BQ、CQ，先利用勾股定理计算出AB=5，设⊙P的半径为R，⊙Q的半径为r，在Rt△PBD中利用勾股定理得到（R-3）2+42=R2，解得R=，则PD=，再利用面积法求出r=，即QD=，然后计算PD+QD即可．

详（1）解：∵AD是边BC上的中线，

∴BD=CD，

∵CE∥AD，

∴AD为△BCE的中位线，

∴CE=2AD=6；

（2）证明：∵BD=CD，∠BAD=∠CAD，AD=AD，

∴△ABD≌△CAD，

∴AB=AC，

∴△ABC为等腰三角形．

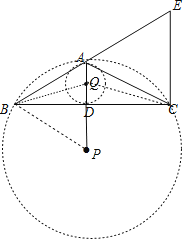
（3）如图，连接BP、BQ、CQ，

在Rt△ABD中，AB==5，

设⊙P的半径为R，⊙Q的半径为r，

在Rt△PBD中，（R-3）2+42=R2，解得R=，

∴PD=PA-AD=-3=，

∵S△ABQ+S△BCQ+S△ACQ=S△ABC，

∴×r×5+×r×8+×r×5=×3×8，解得r=，

即QD=，

∴PQ=PD+QD=+=．

答：△ABC的外接圆圆心P与内切圆圆心Q之间的距离为．