题目内容
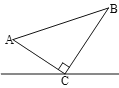
【题目】如图1,将等腰△ABC沿对称轴折叠后,得到△ADC(△ADB),若![]() ,则称等腰△ABC为“长月三角形”ABC.
,则称等腰△ABC为“长月三角形”ABC.
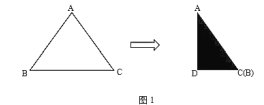
(1)结合题目情境,请你判断“长月三角形”一定会是______三角形.
(2)如图2,C为线段AB上一点,分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE,连接AE、BD交于点O,AE与CD交于点P,CE与BD交于点M.
①求证:![]() ;
;
②求![]() 的度数.
的度数.
【答案】(1)等边;(2)①见解析;②120°
【解析】
(1)利用等腰三角形性质以及含30°的直角三角形进行判断即可.
(2)①利用(1)中结论,易证![]() ,即可解答;
,即可解答;
②利用全等三角形对应角相等的性质,即可解答.
(1)等边;
证明:∵将等腰△ABC沿对称轴折叠
∴AD⊥CD ∴△ADC为直角三角形
∵![]()
∴∠A=30°,∠C=60°
∴等腰△ABC为等边三角形.
∴“长月三角形”一定会是等边三角形.
(2)①由(1)可知,△ACD和△BCE是等边三角形
∴AC=CD,CE=CB,∠ACD=∠BCE=60°
∴∠ACD+∠DCE=∠BCE+∠DCE 即∠ACE=∠BCD
在![]() 和
和![]() 中,
中,
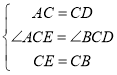
∴![]()
∴AE=BD
②∵![]()
∴∠CAE=∠CDB
∵∠DCA=∠CDB+∠DBC=60°
∴∠DOA=∠CAE+∠DBC=60°
∵∠DOA+∠AOB=180°
∴∠AOB=120°

【题目】数学是神秘奇妙的,数与字母有着密切的联系,字母可以表示数,数可以赋予字母其值,以下是某同学参加校庆举办的“越战越勇”活动的一道思考题,请同学们帮他完成,
(1)填表:
|
| |
用代数式表示 |
| |
|
| |
| ||
|
根据表中计算结果,你发现了什么等式?请写出这个等式
(2)利用(1)中发现的结论,计算![]()
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?