题目内容
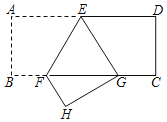
【题目】四边形![]() 是矩形,点
是矩形,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() .
.
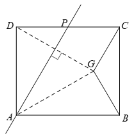
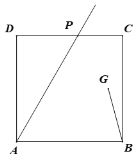
(1)如图,若四边形![]() 是正方形,求
是正方形,求![]() 的度数;
的度数;
(2)连接![]() ,设
,设![]() 探究当
探究当![]() 时a与b的数量关系.
时a与b的数量关系.
【答案】(1)15°;(2)a=![]() b或 a=
b或 a=![]() b
b
【解析】
(1)连接DG,交AP于点E,连接AG,根据对称的性质和正方形的性质,可以求到AG=AB,∠GAB=30°,再结合等腰三角形的性质即可求得答案;
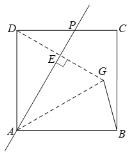
(2)连接DG,AG,先判断△ADG是等边三角形,根据等边三角形的性质和矩形的性质推到△GAB≌△GDC;当∠CGB=120°时,点G可能在矩形ABCD的内部或外部,所以这里需要分两种情况,分别画图求解即可.
(1)解:连接DG,交AP于点E,连接AG,
∵点G与点D关于直线AP对称,
∴AP垂直平分DG,
∴AD=AG.
∵在△ADG中,AD=AG,AE⊥DG,
∴∠PAG=∠PAD=30°.
又∵在正方形ABCD中,AD=AB,∠DAB=∠ABC=90°
∴AG=AB,∠GAB=∠DAB-∠PAD-∠PAG=30°,
∴在△GAB中,∠ABG=∠AGB=![]() =75°
=75°
∴∠GBC=∠ABC-∠ABG=15°
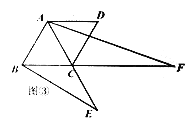
(2)解:连接DG,AG,
由(1)可知,在△ADG中,AD=AG,
∠DAG=∠PAD+∠PAG=60°,
∴△ADG是等边三角形,
∴DG=AG=AD,∠DAG=∠ADG=∠DGA=60°,
又∵ 在矩形ABCD中,AB=DC,∠DAB=∠ADC=∠ABC=90°,
∴∠DAB-∠DAG=∠ADC-∠ADG,
即∠GAB=∠GDC=30°,
∴△GAB≌△GDC,
∴GB=GC;
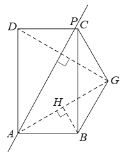
当∠CGB=120°时,点G可能在矩形ABCD的内部或外部,
若点G在矩形ABCD的内部,
∵在△BGC中,GB=GC,∠CGB=120°,
∴∠GBC=![]() =30°,
=30°,
∴∠GBA=∠ABC-∠GBC=90°-30°=60°,
在△ABG中,∠AGB=180°-∠GAB-∠GBA=90°,
∴在Rt△ABG中,cos∠GAB=![]() ,
,
∴a=![]() b,
b,
若点G在矩形ABCD的外部,
在△BGC中,∠GBC=30°,
∴∠ABG=120°,
又∵∠GAB=30°,
∴∠AGB=180°-30°-120°=30°,
∴BA=BG,
过点B作BH⊥AG,垂足为H,
∴AH=![]() AG=
AG=![]() b,
b,
在Rt△ABH中,∠AHB=90°,∠HAB=30°,
∴cos∠HAB=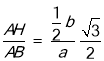 ,
,
∴a=![]() b,
b,
在Rt△ADP中,∠ADP=90°,∠PAD=30°,
∴tan∠PAD=![]() ,
,
∴DP=![]() b;
b;
所以无论点G在矩形ABCD内部还是点G在矩形ABCD外部,都有DP≤DC,均符合题意;
综上,当∠CGB=120°时a与b的数量关系为a=![]() b或 a=
b或 a=![]() b.
b.