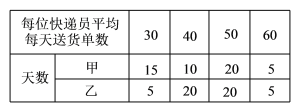题目内容
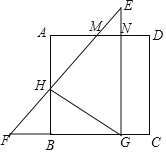
【题目】(12分)如图,在四边形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于点F,连接AF.
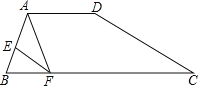
(1)求CF的长;
(2)若∠BFE=∠FAB,求AB的长.
【答案】(1)4;(2)![]() .
.
【解析】
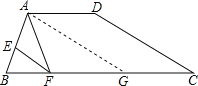
试题(1)作AG∥CD交BC于点G,根据平行四边形的性质可知CG=AD=2,由EF∥AG,AE=2EB,利用平行线分线段成比例定理可求出FG=2,CF=FG+GC即可求出结果;
(2)先证明△BFE∽△BAF,得到![]() ,由BE=
,由BE=![]() AB和BF=1可求出AB.
AB和BF=1可求出AB.
试题解析:解:(1)作AG∥CD交BC于点G,
∵AD∥BC,
∴四边形AGCD是平行四边形,
∴GC=AD,
∵AD=2,
∴GC=2,
∵BC=5,
∴BG=BC﹣GC=5﹣2=3,
∵EF∥DC,AG∥CD,
∴EF∥AG,
∴![]() ,
,
∴![]() ,
,
∵AE=2EB,
∴![]() ,
,
∴![]() ,
,
∵BG=3,
∴FG=2,
∴CF=FG+GC=2+2=4;
(2)∵∠BFE=∠FAB,∠B=∠B,
∴△BFE∽△BAF,
∴![]() ,
,
∴ABBE=BF2,
∴AB![]() AB=BF2,
AB=BF2,
∵BF=BC﹣FG=5﹣4=1,
∴AB=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后郗进行了测试.现将项目选择情况及训练前后篮球定时定点投测试成绩整理作出如下统计图表.
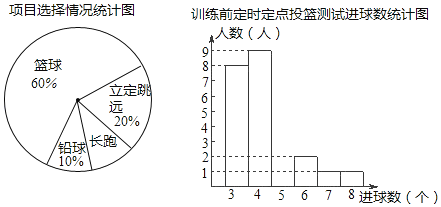
训练后篮球定时定点投篮测试进球数统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题
(1)送择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(2)直接补全“训练前篮球定时定点投测试进球数统计图”;
(3)若全区共有该年级学生4000人,请估计参加训练后篮球定时定点投篮进球数达到6个以上(包含6个)多少人?
【题目】某班“数学兴趣小组”对函数y=![]() ,的图象和性质进行了探究探究过程如下,请补充完成:
,的图象和性质进行了探究探究过程如下,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值.请直接写出m,n的值:m= ;n= .
x | … | ﹣2 | ﹣1 | 0 |
|
|
| n | 2 | 3 | 4 | … |
y | … |
| m | 0 | ﹣1 | ﹣3 | 5 | 3 | 2 |
|
| … |
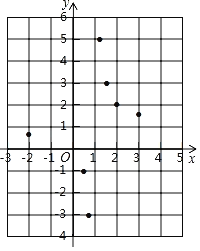
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)通过观察函数的图象,小明发现该函数图象与反比例函数y=![]() (k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,
(k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,![]() )是一组对称点,则其对称中心的坐标为 .
)是一组对称点,则其对称中心的坐标为 .
(5)当2≤x≤4时,关于x的方程kx+![]() =
=![]() 有实数解,求k的取值范围.
有实数解,求k的取值范围.