题目内容
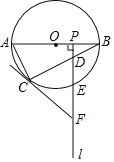
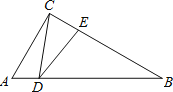
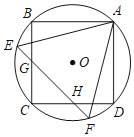
【题目】如图，正方形ABCD和等边△AEF都内接于圆O，EF与BC、CD别相交于点G、H．若AE＝6，则EG的长为（ ）
A.
B.3﹣C.
D.2﹣3
【答案】B
【解析】
连接AC、BD、OF，AC与EF交于P点，则它们的交点为O点，如图，利用正方形和等边三角形的性质得到∠COF＝60°，AC⊥BD，∠BCA＝45°，利用含30度的直角三角形三边的关系得到OP＝
OF＝OC，OP＝
PF＝
，从而得到PC＝OP＝，然后利用△PCG为等腰直角三角形得到PG＝PC＝，从而得到EG的长．
连接AC、BD、OF，AC与EF交于P点，则它们的交点为O点，如图，
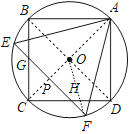
∵正方形ABCD和等边△AEF都内接于圆O，
∴正方形ABCD和等边△AEF都是轴对称图形，直径AC是对称轴，
∴∠COF＝60°，AC⊥BD，AC⊥EF，∠BCA＝45°，
∴PE＝PF＝EF＝3，
在Rt△OPF中，OP＝OF＝OC，
∵OP＝PF＝，
∴PC＝OP＝，
∵△PCG为等腰直角三角形，
∴PG＝PC＝，
∴EG＝PE﹣PG＝3﹣．
故选：B．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行了一次测试（满分50分，成绩均记为整数分），并按测试成绩
（单位：分）分成四类：
类（
），
类（
），
类（
），
类（
）绘制出如图所示的不完整条形统计图，请根据图中信息解答下列问题：
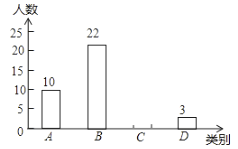
成绩等级 | 人数 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
（1）
______，
_______，
_________；
（2）补全条形统计图；
（3）若该校九年级男生有600名，类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？
