题目内容
【题目】如图,A、B是函数
图象上关于原点对称的两点,且BC//x轴,AC//y轴,△ABC的面积记为S,则( )
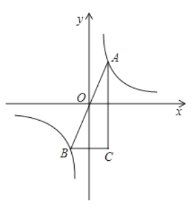
A.S=2B.S=4C.S=8D.S=1
【答案】B
【解析】
连接OC，设AC与x轴交于点D，BC与y轴交于点E．首先由反比例函数
的比例系数k的几何意义，可知△AOD的面积等于
|k|，再由A、B两点关于原点对称，BC∥x轴，AC∥y轴，可知S△AOC=2×S△AOD，S△ABC=2×S△AOC，从而求出结果．
解：连接OC，设AC与x轴交于点D，BC与y轴交于点E．
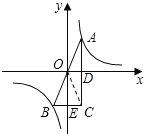
∵A、B两点关于原点对称，BC∥x轴，AC∥y轴，
∴AC⊥x轴，AD=CD，OA=OB．
∴S△COD=S△AOD=×2=1，
∴S△AOC=2，
∴S△BOC=S△AOC=2，
∴S△ABC=S△BOC+S△AOC=4．
故选：B．
练习册系列答案
特高级教师点拨系列答案
相关题目
