题目内容
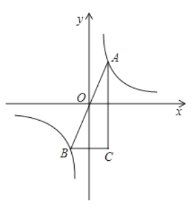
【题目】如图，一次函数
的图与y轴分别交于点A，且反比例函数
的图象在第一象限内的交点为M.
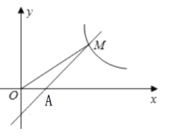
（1）求点M的坐标.
（2）在x轴上是否存在点P，使AM⊥MP？若存在，求出点P的坐标；若不存在，说明理由。
【答案】（1）（2,2）；（2）存在，（6.0）
【解析】
（1）联立方程组，解方程组求解；
（2）过点M（3，4）作MP⊥AM交x轴于点P，由MD⊥BP可求出∠PMD=∠MBD=∠ABO，再由锐角三角函数的定义可得出OP的值，进而可得出结论．
解：（1）由题意，联立方程组得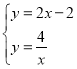
解得：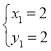
；
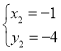
∴M点坐标为（2,2）
（2）过点M（2，2）作MP⊥AM交x轴于点P，
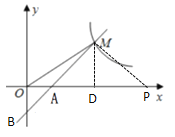
由
可得A（1,0）；B（0，-2）
∵MD⊥BP，
∴∠PMD=∠MAD=∠BAO
∴tan∠PMD=tan∠MAD=tan∠BAO=
∴在Rt△PDM中，
＝2，
∴PD=2MD=4，
∴OP=OD+PD=6
∴在x轴上存在点P，使PM⊥AM，此时点P的坐标为（6，0）
练习册系列答案
阅读快车系列答案
相关题目
