题目内容
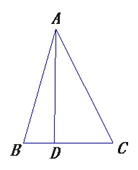
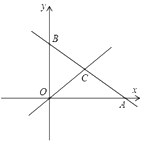
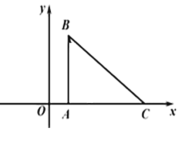
【题目】如图,点![]() 平面直角坐标系的原点,三角形
平面直角坐标系的原点,三角形![]() 中,
中,![]() ,顶点
,顶点![]() 的坐标分别为
的坐标分别为![]() ,且
,且![]() .
.
(1)求三角形![]() 的面积;
的面积;
(2)动点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 方向以每秒
方向以每秒![]() 个单位长度的速度运动,设点
个单位长度的速度运动,设点![]() 的运动时间为t秒.连接
的运动时间为t秒.连接![]() ,请用含t的式子表示三角形
,请用含t的式子表示三角形![]() 的面积;
的面积;
(3)在(2)的条件下,当三角形![]() 的面积为
的面积为![]() 时,直线
时,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,求点
,求点![]() 的坐标
的坐标
【答案】(1)6;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)由非负数的性质求出m、n即可解决问题;
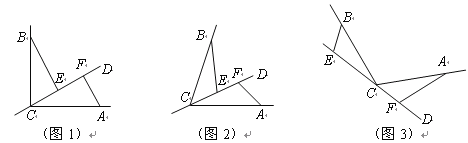
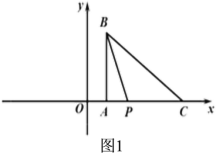
(2)如图1,当点P在线段AC上时,PC=t,AP=4-t,可求出三角形ABP的面积,如图2,当点P在线段CA的延长线上时,PC=t,AP=t-4,可求出三角形ABP的面积.
(3)当点P在线段AC上时,不合题意,当点P在线段CA的延长线上时,![]() t6=
t6=![]() .求出t=9,根据三角形PAB的面积可求出OD的值,则可得解.
.求出t=9,根据三角形PAB的面积可求出OD的值,则可得解.
(1)![]()
![]()
![]()
![]()
![]()
![]() 三角形
三角形![]() 的面积为
的面积为![]()
(2)①如图 1,当点![]() 在线段
在线段![]() 上时,
上时,![]()
三角形![]() 的面积为
的面积为![]()
②如图 2,当点![]() 在CA延长线上时,
在CA延长线上时,![]()
三角形![]() 的面积为
的面积为![]()

(3)①当点![]() 在线段 AC 上时
在线段 AC 上时![]() ,解得
,解得![]() (舍)
(舍)
②如图![]() ,当点
,当点![]() 在CA延长线上时
在CA延长线上时![]() ,解得
,解得![]()
![]()
![]()
![]()
![]() 三角形
三角形![]() 的面积=三角形的
的面积=三角形的![]() 面积+梯形
面积+梯形![]() 的面积
的面积
![]()
解得点![]()
∵![]() 在
在![]() 轴上且在原点
轴上且在原点![]() 的上方,
的上方,
![]() 点
点![]() 的坐标为
的坐标为![]()

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
【题目】某商场用![]() 元购进
元购进![]() 两种新型护服台灯共
两种新型护服台灯共![]() 盏,这两种台灯的进价、标价如下表所示:
盏,这两种台灯的进价、标价如下表所示:
价格 |
|
|
进价(元/盏) |
|
|
标价(元/盏) |
|
|
(1)![]() 两种新型护眼台灯分别购进多少盏?
两种新型护眼台灯分别购进多少盏?
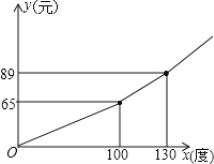
(2)若![]() 型护眼灯按标价的
型护眼灯按标价的![]() 折出售,
折出售,![]() 型护眼灯按标价的
型护眼灯按标价的![]() 折出售,那么这批台灯全部售完后,商场共获利
折出售,那么这批台灯全部售完后,商场共获利![]() 元,请求出表格中
元,请求出表格中![]() 的值
的值