题目内容
【题目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
(1)判断四边形AEMF的形状,并给予证明.
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求四边形AEMF的面积.

【答案】(1)四边形AEMF是正方形;(2)36
【解析】(1)根据折叠的性质可得到∠1=∠3,∠2=∠4,AE=AE,由∠BAC=45°可判断出∠EAF的度数,进而可判断出四边形AEMF的形状;
(2)由图形翻折变换的性质可知,BE=BD,CF=CD,设正方形AEMF的边长是x,在Rt△BMC中利用勾股定理可求出x的值,由正方形的面积公式即可求出其面积.
(1)如图,
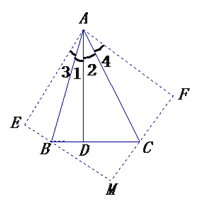
∵AD![]() BC
BC
△AEB是由△ADB折叠所得
∴∠1=∠3,∠E=∠ADB=90°,BE=BD, AE=AD
又∵△AFC是由△ADC折叠所得
∴∠2=∠4,∠F=∠ADC==90°,FC=CD,AF=AD
∴AE=AF
又∵∠1+∠2=45°,
∴∠3+∠4=45°
∴∠EAF==90°
∴四边形AEMF是正方形。
(2)设AD=x,则正方形AEMF的边长为![]()
根据题意知:BE=BD=2, CF=CD=3
∴BM=![]() ; CM=
; CM=![]()
在Rt△BMC中,由勾股定理得:
![]()
∴![]()
![]()
解之得:![]() ,
,![]() (舍去)
(舍去)
∴![]()

 阶梯计算系列答案
阶梯计算系列答案【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行了有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会. 在一个纸盒里装有2个红求和2个白球,除颜色外其他都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表)
甲 超 市
球 | 两红 | 一红一白 | 两白 |
礼金券 | 5 | 10 | 5 |
乙 超 市
球 | 两红 | 一红一白 | 两白 |
礼金券 | 10 | 5 | 10 |
(1)用树状图或列表法表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.