题目内容
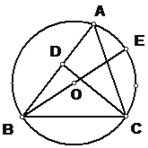
【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.

【答案】(1)∠DAB=135°;(2)四边形ABCD的面积为![]() .
.
【解析】
(1)由于∠B=90°,AB=BC=2,利用勾股定理可求AC,并可求∠BAC=45°,而CD=3,DA=1,易得AC2+DA2=CD2,可证△ACD是直角三角形,于是有∠CAD=90°,从而易求∠BAD;
(2)连接AC,则可以计算△ABC的面积,根据AB、BC可以计算AC的长,根据AC,AD,CD可以判定△ACD为直角三角形,根据AD,CD可以计算△ACD的面积,四边形ABCD的面积为△ABC和△ADC面积之和.
解:(1)连结AC,
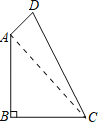
∵∠B=90°,AB=BC=2,
∴![]() ,∠BAC=45°,
,∠BAC=45°,
∵AD=1,CD=3,
∴![]() ,CD2=9,
,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=135°.
(2)在 Rt△ABC中,![]() ,
,
在 Rt△ADC中,![]() .
.
∴![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某影院共有15排座位,第一排有12个座位数,从第2排开始,每一排都比前一排增加2个座位.
(1)请你在下表的空格里填写一个适当的式子.
第1排的座位数 | 第2排的座位数 | 第3排的座位数 | … | 第 |
12 | 14 | 16 | … |
(2)影院最后两排共有多少个座位?
【题目】体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图,如图:
次数 | 频数 |
| 2 |
| |
| 18 |
| 13 |
| 8 |
| |
| 1 |
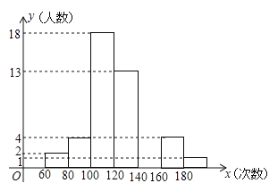
(1)补全频数分布表和频数分布直方图.
(2)上表中组距是__________次,组数是___________组.
(3)跳组次数在![]() 范围的学生有__________人,全班共有___________人.
范围的学生有__________人,全班共有___________人.
(4)若规定跳维次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?