题目内容
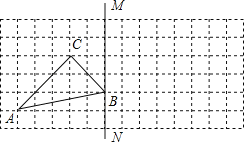
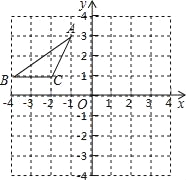
【题目】如图，二次函数y＝x2－4x＋3的图象与x轴交于A，B两点(点B在点A的右侧)，与y轴交于点C，抛物线的对称轴与x轴交于点D.
(1)求点A，点B和点D的坐标；
(2)在y轴上是否存在一点P，使PBC为等腰三角形？若存在，请求出点P的坐标；
(3)若动点M从点A出发，以每秒1个单位长度的速度沿AB向点B运动，同时另一个动点N从点D出发，以每秒2个单位长度的速度在抛物线的对称轴上运动，当点M到达点B时，点M，N同时停止运动，问点M，N运动到何处时，MNB的面积最大，试求出最大面积．
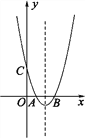(备用图)
【答案】见解析
【解析】试题分析：（1）已知抛物线的一般式，令y=0，可得关于x的方程，解方程可得抛物线与x轴交点的横坐标，从而得到A、B两点坐标，通过配方可得到抛物线的对称轴，从而可得点D的坐标；
（2）先求出BC的长，然后分情况进行讨论即可得；
（3）设点M运动的时间为ts，用含t的式子先表示出BM与DN的长，然后利用三角形的面积公式表示出△MNB的面积，再根据二次函数的性质即可得.
试题解析：(1)当y＝0时，x2－4x＋3＝0.
解得x1=1，x2=3，
∵点B在点A的右侧，∴点A的坐标为（1，0），点B的坐标为（3，0），
∵y=x2-4x+3=(x-2)2-1，
∴点D的坐标为（2，0）；
（2）存在一点P，使△PBC为等腰三角形，
当x=0加法，y=x2-4x+3=3，∴点C的坐标为（0，3），
∴BC=
，
点P中y轴上，当△PBC为等腰三角形时分三种情况讨论，点P位置如图，
①当CP＝CB时，PC＝3
，
∴OP＝OC＋PC＝3＋3
或OP＝PC－OC＝3
－3.
∴P1(0，3＋3
)，P2(0，3－3
)；
②当BP＝BC时，OP＝OC＝3，
∴P3(0，－3)；
③当PB＝PC时，
∵OC＝OB＝3，
∴此时点P与点O重合．
∴P4(0，0)，
综上所述，当点P的坐标为(0，3＋3
)或(0，3－3
)或(0，－3)或(0，0)时，△PBC为等腰三角形；
（3）设点M运动的时间为ts，
∵AB=2，∴BM=2-t，DN=2t，
∴S△MNB=
=-t2+2t=-(t-1)2+1，
∴当t=1时，△MNB的面积最大，最大面积为1，
此时M（2，0），N（2，2）或（2，-2），
∴当点M运动到（2，0），点N运动到（2，2）或（2，-2）时，△MNB的面积最大，最大面积为1.
