题目内容
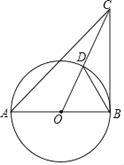
【题目】如图,在△ABC中,AB=BC,∠A=45°,以AB为直径的⊙O交CO于点D.
(1)求证:BC是⊙O的切线;
(2)连接BD,若BD=m,tan∠CBD=n,写出求直径AB的思路.
【答案】见解析
【解析】分析:(1)欲证明BC是⊙O的切线,只需推知∠ABC=90°即可;
(2)①连接AD,利用圆周角定理和等角的余角相等推知∠BAD=∠CBD;②通过解直角Rt△ABD可求AD=![]() ;③在Rt△ABD中,由勾股定理可求AB的长.
;③在Rt△ABD中,由勾股定理可求AB的长.
详解:(1)∵AB=BC,∠A=45°,
∴∠ACB=∠A=45°.
∴∠ABC=90°,
∴AB⊥BC,
∵AB是⊙O的直径,
∴BC是⊙O的切线;
(2)求解思路如下:
①连接AD,
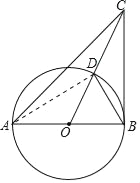
由AB为直径可知,∠ADB=90°,进而可知∠BAD=∠CBD;
②由BD=m,tan∠CBD=n,在Rt△ABD中,可求AD=![]() ;
;
③在Rt△ABD中,由勾股定理可求AB的长.

练习册系列答案
相关题目