Question

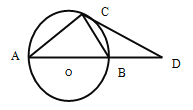
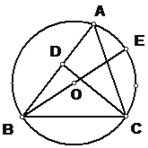
【题目】已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．

（1）求证：AC·BC＝BE·CD；

（2）已知CD＝6、AD＝3、BD＝8，求⊙O的直径BE的长．

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）欲证ACBC=BECD，可以证明△ADC∽△ECB得出；

（2）求⊙O的直径BE的长，由ACBC=BECD知，可在Rt△ACD和Rt△BCD中，根据已知条件求出BC，AC的长即可．

试题解析：（1）证明：连接CE．

∵BE是⊙O的直径，∴∠ECB=90°．

∵CD⊥AB，∴∠ADC=90°，∴∠ECB=∠ADC．

又∵∠A=∠E（同弧所对的圆周角相等），∴△ADC∽△ECB，∴ ，∴ACBC=BECD；

（2）解：∵CD=6，AD=3，BD=8，∴BC===10，∴AC===．

∵ACBC=BECD，∴ ×10=BE6，∴BE=，∴⊙O的直径BE的长是．