题目内容
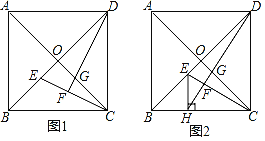
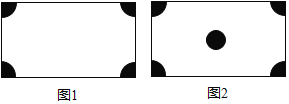
【题目】如图1所示,在一个长方形广场的四角都设计一块半径相同的四分之一圆形的花坛.若广场的长为m米,宽为n米,圆形的半径为r米.
(1)列式表示广场空地的面积.
(2)若广场的长为300米,宽为200米,圆形的半径为30米,求广场空地的面积(计算结果保留π).
(3)如图2所示,在(2)的条件下,若在广场的中间再建一个半径为R的圆形花坛,使广场的空地面积不少于广场总面积的![]() ,求R的最大整数值(π取3.1).
,求R的最大整数值(π取3.1).
【答案】(1)mn﹣πr2,(2)(60000﹣90π)平方米.(3)74米.
【解析】
(1)长方形的面积减去半径为r的圆的面积即可.
(2)把m=300,n=200,r=30代入即可求出空地的面积,
(3)根据面积之间的关系列出不等式,求出不等式的整数解即可.
(1)由题意得,mn﹣πr2,
答:广场空地的面积为(mn﹣πr2)平方米,
(2)把m=300,n=200,r=30代入得,
原式=300×200﹣π×900=(60000﹣900π)平方米,
答:广场空地的面积大约为(60000﹣90π)平方米.
(3)由题意得,
300×200﹣π×302﹣πR2≥300×200×![]() ,
,
解得R≤74.51,
R为最大的整数,
所以R=74米,
答:R的最大整数值为74米.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目