题目内容
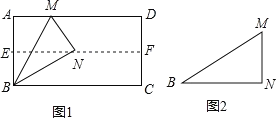
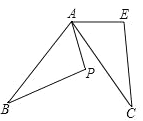
【题目】如图,将ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=8,则AE的长为__.

【答案】![]()
【解析】
过点C作CG⊥AB的延长线于点G,易证△D′CF≌△ECB(ASA),从而可知D′F=EB,CF=CE,设AE=x,在△CEG中,利用勾股定理列出方程即可求出x的值.
过点C作CG⊥AB的延长线于点G,
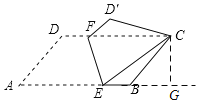
在ABCD中,∠D=∠EBC,AD=BC,∠A=∠DCB,
由于ABCD沿EF对折,
∴∠D′=∠D=∠EBC,∠D′CE=∠A=∠DCB,
D′C=AD=BC,
∴∠D′CF+∠FCE=∠FCE+∠ECB,
∴∠D′CF=∠ECB,且∠D'=∠EBC,D'C=BC
∴△D′CF≌△ECB(ASA)
∴D′F=EB,CF=CE,
∵DF=D′F,
∴DF=EB,AE=CF
设AE=x,则EB=8﹣x,CF=x,
∵BC=4,∠CBG=60°,
∴BG=![]() BC=2,
BC=2,
在Rt△BCG中,由勾股定理可知:CG=![]() ,
,
∴EG=EB+BG=8﹣x+2=10﹣x
在Rt△CEG中,由勾股定理可知:(10﹣x)2+(2![]() )2=x2,
)2=x2,
∴x=![]()
∴AE=![]()
故答案为:![]()

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目