题目内容
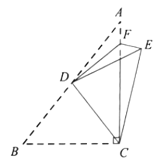
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为斜边
为斜边![]() 上的一点,连接
上的一点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,使点
翻折,使点![]() 落在点
落在点![]() 处,点
处,点![]() 为直角边
为直角边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好与点
恰好与点![]() 重合.若
重合.若![]() ,则
,则![]() _______.
_______.
【答案】![]()
【解析】
根据翻折的性质可得AD=DE,BD=DE,AF=EF,CE=BC,∠A=∠DEF,∠B=∠DEC,可得∠FEC=90°,点D为AB中点,根据直角三角形斜边中线的性质可求出AB的长,利用勾股定理可求出AC的长,根据AF=EF,CF=AC-AF,在Rt△FEC中利用勾股定理列方程求出AF的长即可.
∵![]() 沿
沿![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,
处, ![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好与点
恰好与点![]() 重合,
重合,
∴AD=DE,BD=DE,AF=EF,CE=BC,∠A=∠DEF,∠B=∠DEC,
∵∠ACB=90°,
∴∠FED+∠DEC=∠A+∠B=90°,AD=BD,
∵CD=5,
∴AB=2CD=10,
∵BC=6,
∴AC=![]() =8,CE=BC=6,
=8,CE=BC=6,
在Rt△FEC中,EF=AF,CF=AC-AF=8-AF,
∴CF2=EF2+CE2,即(8-AF)2=AF2+62,
解得:AF=![]() ,
,
故答案为:![]()

 名校课堂系列答案
名校课堂系列答案【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
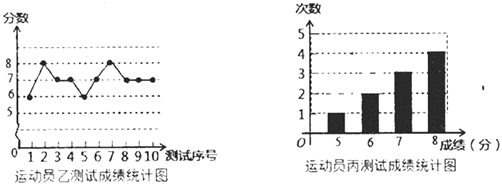
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?
【题目】 某公司的一批某品牌衬衣的质量抽检结果如下:
抽检件数 | 50 | 100 | 200 | 300 | 400 | 500 |
次品件数 | 0 | 4 | 16 | 19 | 24 | 30 |
(1)请结合表格数据直接写出这批衬衣中任抽1件是次品的概率.
(2)如果销售这批衬衣600件,至少要准备多少件正品衬衣供买到次品的顾客退换?