Question

【题目】(1)解方程x2﹣4x=12；

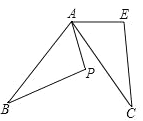
(2)如图，△ABP是由△ACE绕A点旋转得到的，若∠APB=110°，∠B=30°，∠PAC=20°，求旋转角的度数．

Answer 1

【答案】（1）x=6 或 x=﹣2；（2）旋转角的度数为 60°．

【解析】

（1）利用配方法将方程变形为（x-2）2=16，然后直接开平方即可．

（2）充分运用旋转的性质，旋转前后三角形全等，即△ABP≌△ACE，根据对应角相等，三角形内角和定理，对应边的夹角为旋转角．

（1）x2-4x=12

（x-2）2=16

x-2=±4，

x=6或x=-2；

（2）∵∠APB=110°，∠B=30°，

∴∠BAP=180°-110°-30°=40°，

∵∠PAC=20°，

∴∠BAC=∠BAP+∠PAC=60°，

即旋转角的度数为60°．