题目内容
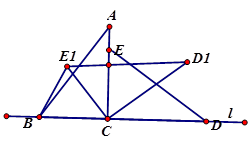
如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l ,则B、E1两点之间的距离为( )
A.3 B.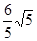 C.
C. 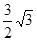 D.
D. 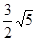

A.3 B.
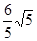 C.
C. 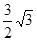 D.
D. 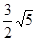
B
试题分析:△ECD绕点C逆时针旋转到△E1CD1位置,
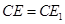 ,D1E1∥l,那么
,D1E1∥l,那么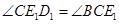 ,
,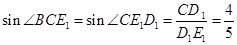 ,在三角形
,在三角形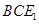 ,由三角函数定义得
,由三角函数定义得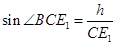 ,所以
,所以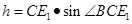 ;直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,那么
;直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,那么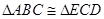 ;∠ACB=∠DCE=90°,BC=CE=3,AC=CD=4,由勾股定理得AB=DE=5;B、E1两点之间的距离即为
;∠ACB=∠DCE=90°,BC=CE=3,AC=CD=4,由勾股定理得AB=DE=5;B、E1两点之间的距离即为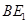 =
=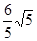
点评:本题考查旋转,勾股定理,解答本题要求考生掌握旋转的特征,熟悉勾股定理的内容

练习册系列答案
相关题目
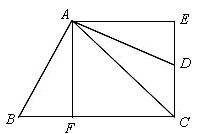
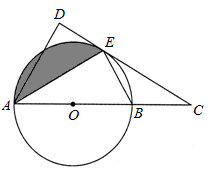

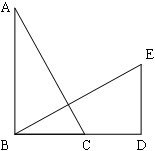
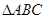 中,
中,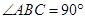 ,点
,点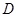 在
在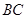 的延长线上,且
的延长线上,且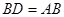 ,过
,过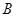 作BE
作BE AC,与
AC,与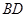 的垂线
的垂线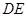 交于点
交于点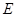 ,
,
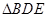 .
.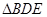 可由
可由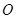 (保留作图痕迹,不写作法).
(保留作图痕迹,不写作法). 中,
中, ,
, 、
、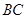 两边的垂直平分线交于点O,则
两边的垂直平分线交于点O,则 的度数是( )
的度数是( )