题目内容
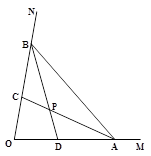
如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD。
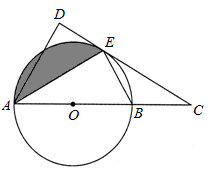

(1)求证:AE平分∠DAC;
(2)若AB=6,∠ABE=60°,①求AD的长;②求出图中阴影部分的面积。


(1)求证:AE平分∠DAC;
(2)若AB=6,∠ABE=60°,①求AD的长;②求出图中阴影部分的面积。
(1)证明∠DAE=∠EAO。∴AE平分∠DAC。(2)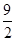 ;
;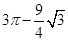
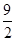 ;
;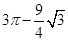
试题分析:(1)证明:连接OE。
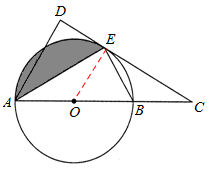
∵CD是⊙O的切线,∴OE⊥CD。
∵AD⊥CD,∴AD∥OE。∴∠DAE=∠AEO。
∵OA=OE,∴∠EAO=∠AEO。
∴∠DAE=∠EAO。∴AE平分∠DAC。
(2)①∵AB是⊙O的直径,∴∠AEB=90°。
∵∠ABE=60°,∴∠EAO=30°。∴∠DAE=∠EAO=30°。
∵AB=6,∴在Rt△ABE中,BE=
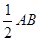 ="3," AE=
="3," AE=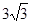
在Rt△ADE中,∵∠DAE=30°,AE=
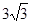 ,∴
,∴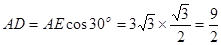 。
。②连接OE ∵∠EAO=∠AEO=30°,∴
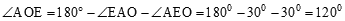 。
。∵OA=OB,∴
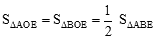 。
。∴
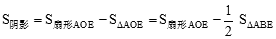
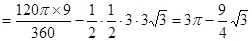 。
。点评:本题考查平分线,三角函数,解答本题需要掌握角平分线的概念和性质,熟悉三角函数的定义,会用三角函数来解题

练习册系列答案
相关题目



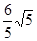 C.
C. 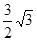 D.
D. 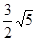
 中,
中,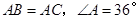 .
.