题目内容
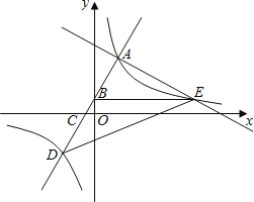
【题目】如图,直线y=2x+b与双曲线y=![]() (k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-
(k>0)交于点A、D,直线AD交y轴、x轴于点B、C,直线y=-![]() +n过点A,与双曲线y=
+n过点A,与双曲线y=![]() (k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
(k>0)的另一个交点为点E,连接BE、DE,若S△ABE=4,且S△ABE:S△DBE=3:4,则k的值为___.
【答案】![]() .
.
【解析】
过点A作AF⊥y轴于点F,过点D作DG⊥y轴于点G,先联立直线AB反比例函数的解析式求出A、D点的横坐标,得到AF与DG,再由三角形的面积比与相似三角形的比例线段得到k与b的关系,进而用b的代数式表示A点坐标,再将其代入AE的解析式中,用b表示n,进而联立AE与反比例函数解析式求出E的坐标,最后根据已知三角形的面积,得到b的方程求得b即可解决问题.
过点A作AF⊥y轴于点F,过点D作DG⊥y轴于点G,
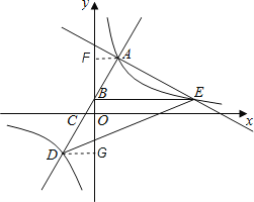
∴AF∥DG,
∴△ABF∽△DBG,
∴![]() ,
,
∵S△ABE:S△DBE=3:4,
∴![]() ,
,
由2x+b=![]() 得,2
得,2![]() +bx-k=0,
+bx-k=0,
解得,x=![]() ,
,
即A点的横坐标为![]() ,D点有横坐标为
,D点有横坐标为![]() ,
,
∴AF=![]() ,DG=
,DG=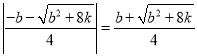 ,
,
∴![]() ,
,
解得,k=6![]() ,
,
∴A点的横坐标为![]() =
=![]() b,纵坐标为
b,纵坐标为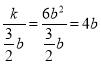 ,
,
∴A(![]() b,4b),
b,4b),
把A(![]() b,4b)代入y=-
b,4b)代入y=-![]() +n中,得n=5b,
+n中,得n=5b,
∴AE的解析式为:y=-![]() +5b,
+5b,
联立方程组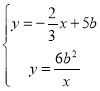 ,
,
解得,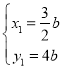 ,
,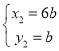 ,
,
∴E(6b,b),
∵B(0,b),
∴BE∥x轴,
∴BE=6b,
∴![]() ,
,
∵S△ABE=4,
∴9![]() =4,
=4,
∴![]() =
=![]() ,
,
∴k=![]() =6×
=6×![]() .
.
故答案为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.