题目内容
【题目】定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形![]() 中,若
中,若![]() ,则称四边形
,则称四边形![]() 为准平行四边形.
为准平行四边形.
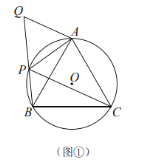
(1)如图①,![]() 是
是![]() 上的四个点,
上的四个点,![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() .求证:四边形
.求证:四边形![]() 是准平行四边形;
是准平行四边形;
(2)如图②,准平行四边形![]() 内接于
内接于![]() ,
,![]() ,若
,若![]() 的半径为
的半径为![]() ,求
,求![]() 的长;
的长;
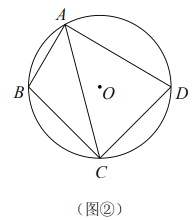
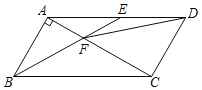
(3)如图③,在![]() 中,
中,![]() ,若四边形
,若四边形![]() 是准平行四边形,且
是准平行四边形,且![]() ,请直接写出
,请直接写出![]() 长的最大值.
长的最大值.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先根据同弧所对的圆周角相等证明三角形ABC为等边三角形,得到∠ACB=60°,再求出∠APB=60°,根据AQ=AP判定△APQ为等边三角形,∠AQP=∠QAP=60°,故∠ACB=∠AQP,可判断∠QAC>120°,∠QBC<120°,故∠QAC≠∠QBC,可证四边形![]() 是准平行四边形;
是准平行四边形;
(2)根据已知条件可判断∠ABC≠∠ADC,则可得∠BAD=∠BCD=90°,连接BD,则BD为直径为10,根据BC=CD得△BCD为等腰直角三角形,则∠BAC=∠BDC=45°,在直角三角形BCD中利用勾股定理或三角函数求出BC的长,过B点作BE⊥AC,分别在直角三角形ABE和△BEC中,利用三角函数和勾股定理求出AE、CE的长,即可求出AC的长.
(3)根据已知条件可得:∠ADC=∠ABC=60°,延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),连接BO交弧AE于D点,则此时BD的长度最大,根据已知条件求出BO、OD的长度,即可求解.
(1)∵![]()
∴∠ABC=∠BAC=60°
∴△ABC为等边三角形,∠ACB=60°
∵∠APQ=180°-∠APC-∠CPB=60°
又AP=AQ
∴△APQ为等边三角形
∴∠AQP=∠QAP=60°
∴∠ACB=∠AQP
∵∠QAC=∠QAP+∠PAB+∠BAC=120°+∠PAB>120°
故∠QBC=360°-∠AQP-∠ACB-∠QAC<120°
∴∠QAC≠∠QBC
∴四边形![]() 是准平行四边形
是准平行四边形
(2)连接BD,过B点作BE⊥AC于E点
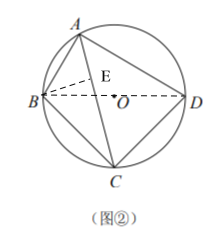
∵准平行四边形![]() 内接于
内接于![]() ,
,![]()
∴∠ABC≠∠ADC,∠BAD=∠BCD
∵∠BAD+∠BCD=180°
∴∠BAD=∠BCD=90°
∴BD为![]() 的直径
的直径
∵![]() 的半径为5
的半径为5
∴BD=10
∵BC=CD,∠BCD=90°
∴∠CBD=∠BDC=45°
∴BC=BD![]() sin∠BDC=10
sin∠BDC=10![]() ,∠BAC=∠BDC=45°
,∠BAC=∠BDC=45°
∵BE⊥AC
∴∠BEA=∠BEC=90°
∴AE=AB![]() sin∠BAC=6
sin∠BAC=6![]()
![]()
∵∠ABE=∠BAE=45°
∴BE=AE=![]()
在直角三角形BEC中,EC=![]()
∴AC=AE+EC=![]()
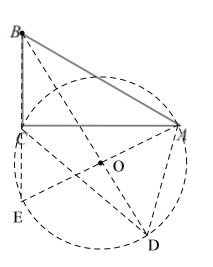
(3)在![]() 中,
中,![]()
∴∠ABC=60°
∵四边形![]() 是准平行四边形,且
是准平行四边形,且![]()
∴∠ADC=∠ABC=60°
延长BC 到E点,使BE=BA,可得三角形ABE为等边三角形,∠E=60°,过A、E、C三点作圆o,因为∠ACE=90°,则AE为直径,点D在点C另一侧的弧AE上(点A、点E除外),此时,∠ADC=∠AEC=60°,连接BO交弧AE于D点,则此时BD的长度最大.
在等边三角形ABE中,∠ACB=90°,BC=2
∴AE=BE=2BC=4
∴OE=OA=OD=2
∴BO⊥AE
∴BO=BE![]() sin∠E=4
sin∠E=4![]()
∴BD=BO+0D=2+![]()
即BD长的最大值为2+![]()

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】为了解某校七年级学生作业时间情况,随机抽取了该校七年级部分学生进行调查,并根据调查结果绘制了如下的统计图.
作业时间分组表(单位:小时)
别 | 作业时间 | 人数 | 频率 |
A | 1≤x≤1.5 | 5 | 0.1 |
B | 1.5≤x≤2 | 20 | b |
C | 2≤x≤2.5 | m | n |
D | x≥2.5 | 7 | 0.14 |
小计 | a | 1 |
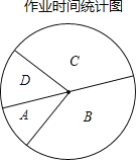
(1)统计图中的a=______;b=______;m=______;n=______.
(2)求出C组的扇形的圆心角度数.
(3)如果该校七年级学生共400名,试估计这400名生作业时间在B组和C组的人数共有多少人?