题目内容
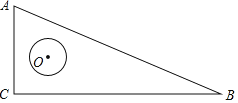
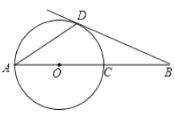
【题目】如图,![]() 是
是![]() 的弦,
的弦,![]() 经过圆心
经过圆心![]() ,交
,交![]() 于点
于点![]() ,
,![]() .
.
(1)直线![]() 是否与
是否与![]() 相切?为什么?
相切?为什么?
(2)连接![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)相切,证明详见解析;(2)15
【解析】
(1)连接OD,根据三角形的内角和求出∠ADB,再根据半径相等得出∠A=∠ADO=30°,即可得出答案;
(2)连接CD,求证△ODC是等边三角形,再证CD=CB,即可得出答案.
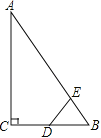
(1)证明:连接OD
∵![]()
∴∠ADB=180°-∠DAB-∠B=120°
又OA=OD
∴∠A=∠ADO=30°
∴∠ODB=∠ADB-∠ADO=90°
∴直线![]() 与
与![]() 相切
相切
(2)连接CD
∵∠A=30°
∴∠DOC=60°
又OD=OC
∴△DOC是等边三角形
∴OD=OC=CD=5,∠ODC=60°
∴∠CDB=∠ODB-∠ODC=30°
又∠B=30°
∴∠B=∠CDB
∴CB=CD=5
∴AB=AC+CB=2OC+CB=10+5=15

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
【题目】观察下表:
x | 0 | 1 | 2 |
ax2 |
| 1 |
|
ax2+bx+c | ﹣3 |
| ﹣3 |
(1)求a、b、c的值,并在表内空格处填入正确的数;
(2)根据上面的结果解答问题:
①在方格纸中画出函数y=ax2+bx+c的图象;
②根据图象回答:当x的取值范围是 时,y≤0?