ΧβΡΩΡΎ»ί
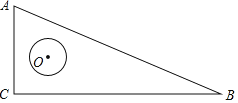
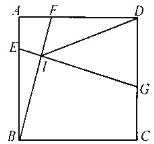
ΓΨΧβΡΩΓΩ»γΆΦΔΌΘ§‘ΎΨΊ–ΈABCD÷–Θ§AB=![]() Θ§AD=3Θ§ΒψE «±ΏADΩΩΫϋAΒΡ»ΐΒ»Ζ÷ΒψΘ§ΒψP «BC―”≥ΛœΏ…œ“ΜΒψΘ§«“EPΓΆEBΘ§ΒψG «BE…œ»Έ“β“ΜΒψΘ§ΙΐGΉςGHΓΈBPΘ§ΫΜEP”ΎΒψHΘ°ΫΪΓςEGH»ΤΒψEΡφ ±’κ–ΐΉΣΠΝΘ®0ΘΦΠΝΘΦ90ΓψΘ©Θ§ΒΟΒΫΓςEMNΘ®MΓΔNΖ÷±π «GΓΔHΒΡΕ‘”ΠΒψΘ©Θ°
Θ§AD=3Θ§ΒψE «±ΏADΩΩΫϋAΒΡ»ΐΒ»Ζ÷ΒψΘ§ΒψP «BC―”≥ΛœΏ…œ“ΜΒψΘ§«“EPΓΆEBΘ§ΒψG «BE…œ»Έ“β“ΜΒψΘ§ΙΐGΉςGHΓΈBPΘ§ΫΜEP”ΎΒψHΘ°ΫΪΓςEGH»ΤΒψEΡφ ±’κ–ΐΉΣΠΝΘ®0ΘΦΠΝΘΦ90ΓψΘ©Θ§ΒΟΒΫΓςEMNΘ®MΓΔNΖ÷±π «GΓΔHΒΡΕ‘”ΠΒψΘ©Θ°
Θ®1Θ©«σBPΒΡ≥ΛΘΜ
Θ®2Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®3Θ©»γΆΦΔΎΒ±ΠΝ=60Γψ ±Θ§ΒψM«ΓΚΟ¬δ‘ΎGH…œΘ§―”≥ΛBMΫΜNP”ΎΒψQΘ§»ΓEPΒΡ÷–ΒψKΘ§Ν§Ϋ”QKΘ°»τΒψG‘ΎœΏΕΈEB…œ‘ΥΕ·Θ§Έ QK «Ζώ”–Ήν–Γ÷ΒΘΩ»τ”–Ήν–Γ÷ΒΘ§«κ«σ≥ωΒψG‘ΥΕ·ΒΫEBΒΡ ≤Ο¥ΈΜ÷Ο ±Θ§QK”–Ήν–Γ÷ΒΦΑΉν–Γ÷Β «Εύ…ΌΘ§»τΟΜ”–Ήν–Γ÷ΒΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©PB=4ΘΜΘ®2Θ©![]() =
=![]() ΘΜΘ®3Θ©ΒψG‘ΥΕ·ΒΫEBΒΡ÷–ΒψΈΜ÷Ο ±Θ§QK”–Ήν–Γ÷ΒΘ§Ήν–Γ÷ΒΈΣ1Θ°
ΘΜΘ®3Θ©ΒψG‘ΥΕ·ΒΫEBΒΡ÷–ΒψΈΜ÷Ο ±Θ§QK”–Ήν–Γ÷ΒΘ§Ήν–Γ÷ΒΈΣ1Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Ι¥Ι…Ε®άμΒΟBE=2Θ§“Ή÷ΛΓςBAEΓΉΓςPEBΘ§¥”ΕχΒΟ![]() =
=![]() Θ§Φ¥Ω…«σΫβΘΜ
Θ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©”…tanΓœABE=![]() =
=![]() Θ§Ω…ΒΟΓœABE=30ΓψΘ§ΫαΚœ–ΐΉΣΒΡ–‘÷ ΒΟPE=
Θ§Ω…ΒΟΓœABE=30ΓψΘ§ΫαΚœ–ΐΉΣΒΡ–‘÷ ΒΟPE=![]() EBΘ§EN=
EBΘ§EN=![]() EMΘ§ΓœBEM=ΓœPENΘ§ΫχΕχΒΟ≥ωΓςBEMΓΉΓςPENΘ§Φ¥Ω…«σΫβΘΜ
EMΘ§ΓœBEM=ΓœPENΘ§ΫχΕχΒΟ≥ωΓςBEMΓΉΓςPENΘ§Φ¥Ω…«σΫβΘΜ
Θ®3Θ©»ΓPBΒΡ÷–ΒψOΘ§Ν§Ϋ”OQΘ§OKΘ°…ηBQΫΜPE”ΎJΘ§“ΉΒΟBEJ=ΓœPQJ=90ΓψΘ§¥”ΕχΒΟΒΫOQ =2Θ§OK=1Θ§”…QKΓίOQ-OKΘ§Ω…ΒΟQKΒΡΉν–Γ÷ΒΈΣ1Θ§¥Υ ±OΘ§KΘ§QΙ≤œΏΘ§»ΜΚσΗυΨίΠΝ=60Γψ÷ΛΟςEGM «Β»±Ώ»ΐΫ«–ΈΘ§«σ≥ωΓœEBM=30ΓψΘ§ΓœGMB=30ΓψΦ¥Ω…ΒΟΫβΘ°
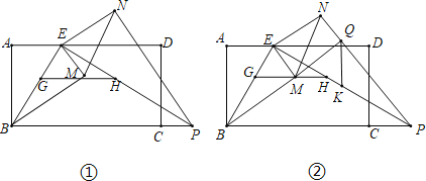
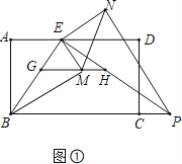
Θ®1Θ©»γΆΦΔΌ÷–Θ§
ΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§
ΓύΓœA=ΓœABC=90ΓψΘ§
ΓΏAE=![]() AD=1Θ§AB=
AD=1Θ§AB=![]() Θ§
Θ§
ΓύBE=![]() =2Θ§
=2Θ§
ÿBEâPEȧ
ΓύΓœPEB=90ΓψΘ§
ΓύΓœABE+ΓœCBE=90ΓψΘ§ΓœCBE+ΓœEPB=90ΓψΘ§
ΓύΓœABE=ΓœEPBΘ§
ΓΏΓœA=ΓœBEP=90ΓψΘ§
ΓύΓςBAEΓΉΓςPEBΘ§
Γύ![]() =
=![]() Θ§
Θ§
ΓύPB=![]() =4ΘΜ
=4ΘΜ
Θ®2Θ©ΓΏ‘ΎRtΓςABE÷–Θ§ tanΓœABE=![]() =
=![]() Θ§
Θ§
ΓύΓœABE=30ΓψΘ§
ΓΏΓœABC=90ΓψΘ§
ΓύΓœEBC=60ΓψΘ§
ÿGHøBCȧ
ΓύΓœEGH=ΓœEBC=ΓœEMN=60ΓψΘ§
ΓΏΓœMEN=ΓœGEH=90ΓψΘ§
ΓύPE=![]() EBΘ§EN=
EBȧEN=![]() EMȧ
EMȧ
Γύ![]() =
=![]() =
=![]() Θ§
Θ§
ΓΏΓœPEB=ΓœMEN=90ΓψΘ§
ΓύΓœBEM=ΓœPENΘ§
ΓύΓςBEMΓΉΓςPENΘ§
Γύ![]() =
=![]() =
=![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦ2÷–Θ§»ΓPBΒΡ÷–ΒψOΘ§Ν§Ϋ”OQΘ§OKΘ°…ηBQΫΜPE”ΎJΘ°
ΓΏΓςBEMΓΉΓςPENΘ§
ΓύΓœEBM=ΓœEPNΘ§
ΓΏΓœBJE=ΓœPJQΘ§
ΓύΓœBEJ=ΓœPQJ=90ΓψΘ§
ÿBO=OPȧ
ΓύOQ=![]() PB=2Θ§
PB=2Θ§
ÿPO=OBȧPK=KEȧ
ΓύOK=![]() BE=1Θ§
BE=1Θ§
ΓύQKΓίOQ-OK=1Θ§
ΓύQKΒΡΉν–Γ÷ΒΈΣ1Θ§¥Υ ±OΘ§KΘ§QΙ≤œΏΘ§
ΓύOQΓΈBEΘ§
ΓύΓœQOP=ΓœEBP=60ΓψΘ§
ΓΏΠΝ=60Γψ ±Θ§ΒψM«ΓΚΟ¬δ‘ΎGH…œΘ§
ΓύΓœEGM=60ΓψΘ§
ΓύEGM «Β»±Ώ»ΐΫ«–ΈΘ§
”÷ΓΏOQ=OBΘ§
ΓύΓœOBQ=![]() ΓΝ60Γψ=30ΓψΘ§
ΓΝ60Γψ=30ΓψΘ§
ΓύΓœEBM=ΓœEBP-ΓœOBQ=60Γψ-30Γψ=30ΓψΘ§
ΓύΓœGMB=ΓœEGM-ΓœEBM=60Γψ-30Γψ=30ΓψΘ§
ΓύBG=GM=GEΘ§
ΓύΒψG «BEΒΡ÷–ΒψΘ§
Ήέ…œΥυ ωΘΚΒψG‘ΥΕ·ΒΫEBΒΡ÷–ΒψΈΜ÷Ο ±Θ§QK”–Ήν–Γ÷ΒΘ§Ήν–Γ÷ΒΈΣ1Θ°


 άΦΆΑΌΆ®ΤΎΡ©ΫπΨμœΒΝ–¥πΑΗ
άΦΆΑΌΆ®ΤΎΡ©ΫπΨμœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΙέ≤λœ¬±μΘΚ
x | 0 | 1 | 2 |
ax2 | ΓΓ ΓΓ | 1 | ΓΓ ΓΓ |
ax2+bx+c | ©¹3 | ΓΓ ΓΓ | ©¹3 |
Θ®1Θ©«σaΓΔbΓΔcΒΡ÷ΒΘ§≤Δ‘Ύ±μΡΎΩ’Ηώ¥ΠΧν»κ’ΐ»ΖΒΡ ΐΘΜ
Θ®2Θ©ΗυΨί…œΟφΒΡΫαΙϊΫβ¥πΈ ΧβΘΚ
ΔΌ‘ΎΖΫΗώ÷Ϋ÷–Μ≠≥ωΚ· ΐyΘΫax2+bx+cΒΡΆΦœσΘΜ
ΔΎΗυΨίΆΦœσΜΊ¥πΘΚΒ±xΒΡ»Γ÷ΒΖΕΈß «ΓΓ ΓΓ ±Θ§yΓή0ΘΩ

ΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥–ΘΤΏΡξΦΕ―ß…ζΉς“Β ±Φδ«ιΩωΘ§ΥφΜζ≥ι»ΓΝΥΗΟ–ΘΤΏΡξΦΕ≤ΩΖ÷―ß…ζΫχ––Βς≤ιΘ§≤ΔΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΝΥ»γœ¬ΒΡΆ≥ΦΤΆΦΘ°
Ής“Β ±ΦδΖ÷Ήι±μΘ®ΒΞΈΜΘΚ–Γ ±Θ©
±π | Ής“Β ±Φδ | »Υ ΐ | ΤΒ¬ |
A | 1ΓήxΓή1.5 | 5 | 0.1 |
B | 1.5ΓήxΓή2 | 20 | b |
C | 2ΓήxΓή2.5 | m | n |
D | xΓί2.5 | 7 | 0.14 |
–ΓΦΤ | a | 1 |
Θ®1Θ©Ά≥ΦΤΆΦ÷–ΒΡa=______ΘΜb=______ΘΜm=______ΘΜn=______Θ°
Θ®2Θ©«σ≥ωCΉιΒΡ…»–ΈΒΡ‘≤–ΡΫ«Ε» ΐΘ°
Θ®3Θ©»γΙϊΗΟ–ΘΤΏΡξΦΕ―ß…ζΙ≤400ΟϊΘ§ ‘ΙάΦΤ’β400Οϊ…ζΉς“Β ±Φδ‘ΎBΉιΚΆCΉιΒΡ»Υ ΐΙ≤”–Εύ…Ό»ΥΘΩ