题目内容
如图所示,一张矩形纸片沿BC折叠,顶点A落在点A′处,再过点A′折叠使折痕DE∥BC,若AB=4,AC=3,则△ADE的面积是 ★ .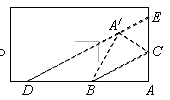

24
分析:沿BC折叠,顶点A落在点A′处,根据折叠的性质得到BC垂直平分AA′,即AF=
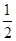 AA′,又DE∥BC,得到△ABC∽△ADE,再根据相似三角形面积的比等于相似比的平方即可求出三角形ADE的面积.
AA′,又DE∥BC,得到△ABC∽△ADE,再根据相似三角形面积的比等于相似比的平方即可求出三角形ADE的面积.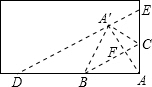
解:连AA′,交BC于点F,如图,
∵沿BC折叠,顶点A落在点A′处,
∴BC垂直平分AA′,即AF=
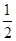 AA′,
AA′,又∵DE∥BC,
∴△ABC∽△ADE,
S△ABC:S△ADE=AF2:AA′2=1:4,
∴S△ADE=4S△ABC=4?
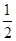 ?4?3=24.
?4?3=24.故答案为24.

练习册系列答案
相关题目

 不小于3cm吗?请说明理由.
不小于3cm吗?请说明理由.

 的值是 .
的值是 .
 平分
平分 ,交
,交 于点
于点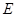 ,点
,点 在边
在边 上.
上.
 ,那么
,那么 和
和 相等吗?证明你的结论
相等吗?证明你的结论 .
. ,那么
,那么 中,点F在边BC上,E在边BA的延长线上.
中,点F在边BC上,E在边BA的延长线上. 按顺时针方向旋转后恰好与
按顺时针方向旋转后恰好与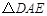 重合.则旋转中心是点 ;
重合.则旋转中心是点 ; ,求四边形
,求四边形 的面积.
的面积. 
