题目内容
【题目】目前中学生带手机进校园现象越来越受到社会关注,针对这种现象,某校数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对),并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题: 
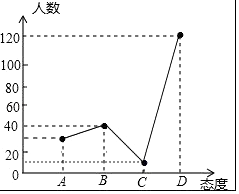
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)根据抽样调查结果,请你估计1万名中学生家长中有多少名家长持反对态度;
(4)在此次调查活动中,初三(1)班和初三(2)班各有2位家长对中学生带手机持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.
【答案】
(1)解:共调查的中学生家长数是:40÷20%=200(人)
(2)解:扇形C所对的圆心角的度数是:360°×(1﹣20%﹣15%﹣60%)=18°
如图所示:
(3)解:根据题意得:
10000×60%=6000(人),
答:10000名中学生家长中有6000名家长持反对态度
(4)解:设初三(1)班两名家长为A1,A2,初三(2)班两名家长为B1,B2,
画树状图为:
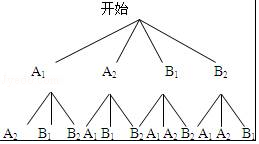
共有12种等可能的结果数,其中2人来自不同班级共有8种,
所以选出的2人来自不同班级的概率= ![]() =
= ![]()
【解析】解:(2)C类的人数是:200×(1﹣20%﹣15%﹣60%)=10(人), 补图如下:
(1)用B类的人数除以它所占的百分比即可得到调查的总人数;(2)用360°乘以C类所占的百分比得到扇形C所对的圆心角的度数,再计算出C类人数,然后补全条形统计图;(3)用10000乘以D类的百分比可估计持反对态度的家长的总数;(4)画树状图展示所有12种等可能的结果数,再找出2人来自不同班级的结果数,然后根据概率公式求解.

 轻松课堂单元期中期末专题冲刺100分系列答案
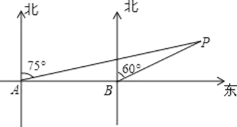
轻松课堂单元期中期末专题冲刺100分系列答案【题目】如图,某轮船由西向东航行,在 A 处测得小岛 P 的方位是北偏东 75°,又继续航行 8 海里后,在 B 处测得小岛 P 的方位是北偏东 60°,则此时△ABP 的面积为______平方海里.
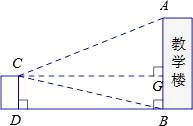
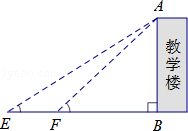
【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)