题目内容
【题目】乘法公式的探究及应用.
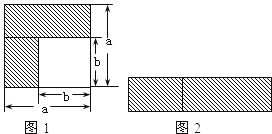
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
【答案】(1)a2﹣b2(2)a﹣b,a+b,(a+b)(a﹣b)(3)99.96(4)①99.96②4m2﹣n2+2np﹣p2
【解析】
试题分析:(1)利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便简单的计算.
解:(1)利用正方形的面积公式可知:阴影部分的面积=a2﹣b2;
故答案为:a2﹣b2;
(2)由图可知矩形的宽是a﹣b,长是a+b,所以面积是(a+b)(a﹣b);
故答案为:a﹣b,a+b,(a+b)(a﹣b);
(3)(a+b)(a﹣b)=a2﹣b2(等式两边交换位置也可);
故答案为:(a+b)(a﹣b)=a2﹣b2;
(4)①解:原式=(10+0.2)×(10﹣0.2),
=102﹣0.22,
=100﹣0.04,
=99.96;
②解:原式=[2m+(n﹣p)]×[2m﹣(n﹣p)],
=(2m)2﹣(n﹣p)2,
=4m2﹣n2+2np﹣p2.

 名校课堂系列答案
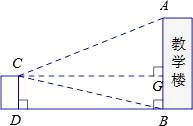
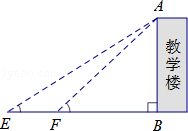
名校课堂系列答案【题目】某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
课题 | 测量教学楼高度 | |
方案 | 一 | 二 |
图示 |
|
|
测得数据 | CD=6.9m,∠ACG=22°,∠BCG=13°, | EF=10m,∠AEB=32°,∠AFB=43° |
参考数据 | sin22°≈0.37,cos22°≈0.93, | sin32°≈0.53,cos32°≈0.85,tan32°≈0.62 |
请你选择其中的一种方法,求教学楼的高度(结果保留整数)