题目内容
【题目】某市计划在十二年内通过公租房建设,解决低收入人群的住房问题.已知前7年,每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系构成一次函数(1≤x≤7且x为整数),且第一和第三年竣工投入使用的公租房面积分别为![]() 和
和![]() 百万平方米;后5年每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系是y=﹣
百万平方米;后5年每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系是y=﹣![]() x+
x+![]() (7<x≤12且x为整数).
(7<x≤12且x为整数).
(1)已知第6年竣工投入使用的公租房面积可解决20万人的住房问题,如果人均住房面积,最后一年要比第6年提高20%,那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题?
(2)受物价上涨等因素的影响,已知这12年中,每年竣工投入使用的公租房的租金各不相同,且第一年,一年38元/m2,第二年,一年40元/m2,第三年,一年42元/m2,第四年,一年44元/m2……以此类推,分析说明每平方米的年租金和时间能否构成函数,如果能,直接写出函数解析式;
(3)在(2)的条件下,假设每年的公租房当年全部出租完,写出这12年中每年竣工投入使用的公租房的年租金W关于时间x的函数解析式,并求出W的最大值(单位:亿元).如果在W取得最大值的这一年,老张租用了58m2的房子,计算老张这一年应交付的租金.
【答案】(1)最后一年可解决12.5万人的住房问题;(2)m=2x+36(1≤x≤12);(3)老张这一年应交租金为2436元.
【解析】(1)利用待定系数法求出一次函数解析式,代入计算即可;
(2)根据函数的概念判断即可;
(3)分1≤x≤7、7<x≤12两种情况列出函数解析式,根据二次函数的性质解答.
(1)设y=kx+b(1≤x≤7),
由题意得,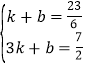 ,解得:
,解得: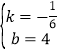 ,
,
∴y=﹣![]() x+4(1≤x≤7),
x+4(1≤x≤7),
∴x=6时,y=﹣![]() ×6+4=3,
×6+4=3,
∴300÷20=15,15×(1+20%)=18,
又x=12时,y=﹣![]() ×12+
×12+![]() =
=![]() ,
,
∴![]() ×100÷18=12.5万人,
×100÷18=12.5万人,
所以最后一年可解决12.5万人的住房问题;
(2)由于每平方米的年租金和时间都是变量,且对于每一个确定的时间x的值,每平方米的年租金m都有唯一的值与它对应,所以它们能构成函数,
由题意知m=2x+36(1≤x≤12);
(3)W=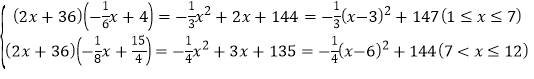 ,
,
∵当x=3时,Wmax=147,
x=8时Wmax=143,147>143,
∴当x=3时,年租金最大,Wmax=1.47亿元,
当x=3时,m=2×3+36=42元,
58×42=2436元,
答:老张这一年应交租金为2436元.