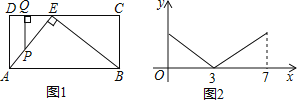Question

【题目】Rt△ABC中，∠ACB＝90°，AC＝3，BC＝7，点P是边AC上不与点A、C重合的一点，作PD∥BC交AB边于点D．

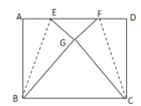
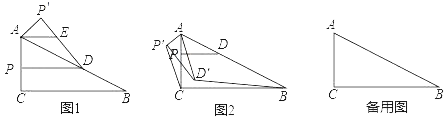
（1）如图1，将△APD沿直线AB翻折，得到△AP'D，作AE∥PD．求证：AE＝ED；

（2）将△APD绕点A顺时针旋转，得到△AP'D'，点P、D的对应点分别为点P'、D'，

①如图2，当点D'在△ABC内部时，连接P′C和D'B，求证：△AP'C∽△AD'B；

②如果AP：PC＝5：1，连接DD'，且DD'＝AD，那么请直接写出点D'到直线BC的距离．

Answer 1

【答案】(1)见解析；（2）①见解析；②点D'到直线BC的距离为或

【解析】

（1）由折叠的性质和平行线的性质可得∠EAD＝∠ADP＝∠ADP'，即可得AE＝DE；

（2）①由题意可证△APD∽△ACB，可得，由旋转的性质可得AP＝AP'，AD＝AD'，∠PAD＝∠P'AD'，即∠P'AC＝∠D'AB，，则△AP'C∽△AD'B；②分点D'在直线BC的下方和点D'在直线BC的上方两种情况讨论，根据平行线分线段成比例，可求PD＝，通过证明△AMD'≌△DPA，可得AM＝PD＝，即可求点D'到直线BC的距离．

证明：（1）∵将△APD沿直线AB翻折，得到△AP'D，

∴∠ADP'＝∠ADP，

∵AE∥PD，

∴∠EAD＝∠ADP，

∴∠EAD＝∠ADP'，

∴AE＝DE

（2）①∵DP∥BC，

∴△APD∽△ACB，

∴ ，

∵旋转，

∴AP＝AP'，AD＝AD'，∠PAD＝∠P'AD'，

∴∠P'AC＝∠D'AB，，

∴△AP'C∽△AD'B

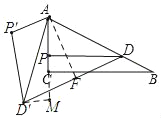
②若点D'在直线BC下方，如图，过点A作AF⊥DD'，过点D'作D'M⊥AC，交AC的延长线于M，

∵AP：PC＝5：1，

∴AP：AC＝5：6，

∵PD∥BC，

∴=，

∵BC＝7，

∴PD＝，

∵旋转，

∴AD＝AD'，且AF⊥DD'，

∴DF＝D'F＝D'D，∠ADF＝∠AD'F，

∵cos∠ADF＝＝ = ，

∴∠ADF＝45°，

∴∠AD'F＝45°，

∴∠D'AD＝90°

∴∠D'AM+∠PAD＝90°，

∵D'M⊥AM，

∴∠D'AM+∠AD'M＝90°，

∴∠PAD＝∠AD'M，且AD'＝AD，∠AMD'＝∠APD，

∴△AD'M≌△DAP（AAS）

∴PD＝AM＝，

∵CM＝AM﹣AC＝﹣3，

∴CM＝，

∴点D'到直线BC的距离为

若点D'在直线BC的上方，如图，过点D'作D'M⊥AC，交CA的延长线于点M，

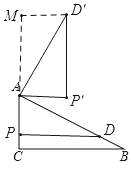
同理可证：△AMD'≌△DPA，

∴AM＝PD＝，

∵CM＝AC+AM，

∴CM＝3+＝，

∴点D'到直线BC的距离为

综上所述：点D'到直线BC的距离为或；