题目内容
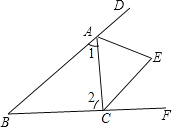
【题目】如图，在△ABC中，∠B=48°，三角形的外角∠DAC和∠ACF的平分线交于点E，∠AEC等于（ ）
A．56° B．66° C．76° D．无法确定
【答案】B
【解析】
试题分析：根据三角形内角和定理、角平分线的定义以及三角形外角定理求得
∠DAC+∠ACF=（∠B+∠B+∠1+∠2）=114°；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数．
解：∵三角形的外角∠DAC和∠ACF的平分线交于点E，
∴∠EAC=∠DAC，∠ECA=∠ACF，
∵∠DAC=∠B+∠2，∠ACF=∠B+∠1
∴∠DAC+∠ACF=（∠B+∠2）+（∠B+∠1）=（∠B+∠B+∠1+∠2），
∵∠B=48°（已知），∠B+∠1+∠2=180°（三角形内角和定理），
∴∠DAC+
∠ACF=114°
∴∠AEC=180°﹣（∠DAC+∠ACF）=66°．
故选B．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
