题目内容
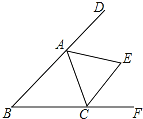
【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,CD平分∠ACB.

(1)尺规作图:作线段AB的垂直平分线l;
(要求:保留作图痕迹,不写作法)
(2)记直线l与AB,CD的交点分别是点E,F.当AC=4时,求EF的长.
【答案】(1)见解析;(2)4.
【解析】
(1)利用尺规作出线段AB的垂直平分线即可.
(2)连接EC,想办法证明EF=EC即可解决问题.
(1)如图所示,直线l是所求作的线段AB的垂直平分线.
(2)解:连接EC.
∵∠ACB=90°,∠B=30°,AC=4,
∴AC=![]() AB,∠A=60°,
AB,∠A=60°,
∴AB=8,
∵EF是AB的垂直平分线,
∴AE=![]() AB=4,∠AEF=90°,
AB=4,∠AEF=90°,
∴AE=AC,
∴△AEC是等边三角形,
∴∠AEC=∠ACE=60°,EC=AC=4,
∴∠FEC=∠AEF+∠AEC=150°,
∵CD平分∠ACB,
∴∠ACF=![]() ∠ACB=45°,
∠ACB=45°,
∴∠ECF=∠ECA-∠FCA=15°,
∴∠EFC=180°-∠FEC-∠ECF=15°=∠ECF,
∴EF=EC=4.

练习册系列答案
相关题目