题目内容
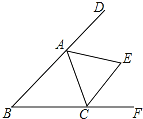
【题目】定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
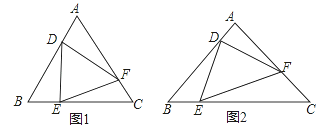
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上动点,且AD=BE=CF.
求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=![]() ,求CF和AD的长.
,求CF和AD的长.
【答案】(1)证明见解析(2)2
【解析】
(1)只要证明△DAF≌△EBD≌△FCE,可得DE=EF=DF,推出△DEF是等边三角形,推出∠DEF=∠EDF=∠B=∠A=60°,推出△DEF∽△ABC.可得△DEF是△ABC的子三角形;
(2)如图2中,作EH⊥AB于H.首先证明△DEF是等腰直角三角形,由△DEH≌△DFA,推出AD=HE,由△BEH是等腰直角三角形,推出HE=![]() ×
×![]() =1,推出AD=1,由△BDE∽△CEF,可得
=1,推出AD=1,由△BDE∽△CEF,可得![]() ,由此即可求出CF.
,由此即可求出CF.
(1)证明:如图1中,
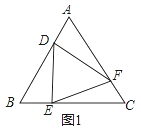
∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵AD=BE=CF,
∴AF=BD=CE,
∴△DAF≌△EBD≌△FCE,
∴DE=EF=DF,
∴△DEF是等边三角形,
∴∠DEF=∠EDF=∠B=∠A=60°,
∴△DEF∽△ABC.
∴△DEF是△ABC的子三角形.
(2)如图2中,作EH⊥AB于H.
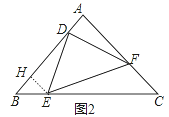
∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵△DEF是△ABC的子三角形,
∴△DEF∽△ABC,
∴DE=DF,∠EDF=90°,
∴∠ADF+∠AFD=90°,∠ADF+∠EDH=90°,
∴∠EDH=∠AFD,
∵∠DHE=∠A=90°,
∴△DEH≌△DFA,
∴AD=HE,
∵△BEH是等腰直角三角形,
∴HE=![]() ×
×![]() =1,
=1,
∴AD=1,
∵∠DEC=∠DEF+∠FEC=∠B+∠BDE,
∵∠B=∠DEF=45°,
∴△BDE∽△CEF,
∴![]() ,
,
∴CF=2.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案